Beatles’ın 1964 yılında yaptığı “A Hard Day’s Night” adlı şarkıyı bilenler olacaktır. Bu şarkı grubun görece daha az dinlenen şarkılarından biridir. Ancak yine de şarkı, müzik tarihinin belki de en büyük gizemlerinden birini 45 yılı aşkın bir süre taşımıştır. Şarkının gizemi giriş kısmının bir türlü yeniden çalınamayan akoru ile ilgilidir.

Giriş kısmında, grubun gitaristleri George Harrison, John Lennon ve Paul McCartney gitarlarına hafifçe dokunarak bir ses çıkarırlar. Kısa bir sessizlikten sonra ise şarkı başlar. Bir akorun nasıl bir gizem olabilir ki? Ancak unutmayın bu tarihin en ünlü gruplarından birinin çaldığı bir akordu. Bunun sonucunda zaman içinde bu akor sadece bir gizem değil, müzisyenler arasında favori tartışma konusu haline geldi.
Daha sonra müzik uzmanları konuya el attı. Stüdyolarda en gelişmiş tekniklerle aynı sesi çıkartmaya çalıştılar. Ancak şarkının giriş notası tüm denemelere rağmen aynı tınıda oluşturulamadı. Nihayetinde 45 yıl boyunca gizem sürdü.
A Hard Day’s Night’s Şarkısının Gizemi Fourier Dönüşümü İLe Çözülecekti
Müzikteki en ünlü akorun tam olarak nasıl çalındığından kimse emin değilken 2004 yılında, albümün 40. yıl dönümü kutlamaları zamanında profesör Jason Brown konuya farklı bir biçimde yaklaşmaya karar verdi. Gizemi çözmek için elbette herkes gibi eline 3 adet gitar alıp deneme yapmadı. Kendisi müziğin gizemini, matematik yardımıyla çözmenin bir yolu olup olmadığını düşünmeye başladı.
Bunun neticesinde aklına 19. yüzyılın büyük Fransız matematikçilerinden Joseph Fourier’ın “Fourier dönüşümü” adlı formülünü kullanmak geldi. Fourier Dönüşümü ismi size ilk etapta tuhaf gelecektir. Ancak aslında yaptığı şey oldukça basittir.
Elinizde bir kağıt banknot varsa ve minibüse bindiğiniz zaman şoförün bu paraya itiraz edeceğini bilirsiniz. Bu nedenle de paranızı bir yerlerde bozdurmak zorunda kalırsınız. Bir kağıt para karşılığında bir sürü bozuk para elde edersiniz. Harcamanızı yaptıktan sonra da bozuk paralarınızı bir yerlerde yeniden bütünlersiniz.
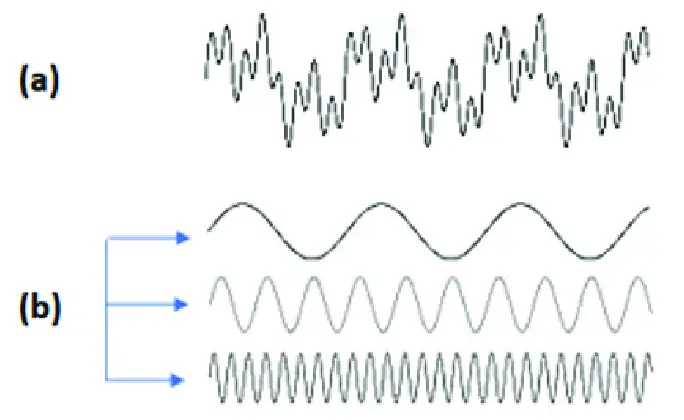
İşte Fourier Dönüşümü de tam olarak aslında bu işi yapar. Ancak paralar ile değil bu sefer dalgalar ile uğraşır. Karmaşık dalgaları alır ve basit sinüs dalgalara ayırır. Daha sonrasında da basit dalgaları tek bir karmaşık dalga olacak biçimde birleştirir.
Sonucunda Gizem Çözülüyor
Jason Brown, Fourier dönüşümü sayesinde ve elbette gelişmiş bilgisayar yazılımları kullanarak Beatles’ın giriş akorunu öncelikle yapı taşlarına ayırdı. Bu sayede George, John ve Paul’ün gitarlarından çıkan notaları ayrı ayrı analiz edilir hale geldi. Ancak tüm bu çabalardan sonra bile bir şeyler hala yanlıştı. Dr Brown verilerini hangi şekilde düzenlerse düzenlesin, akoru çaldığı varsayılan enstrümanlarla tam olarak aynı sesi elde edemedi. Bu ses üç gitardan gelmiyor gibiydi.

En sonunda doğru cevabı buldu. Ortada 4. bir enstrüman vardı. O da bir piyanoydu. Muhtemelen Beatles’ın kompozitörü George Martin tarafından çalınan ve Fa notasına basan bir piyano!

Kaynaklar ve ileri okumalar:
- A Hard Day’s Night: Solving a Beatles mystery with mathematics; Yaınlanma tarihi: 11 Kasım 2017. Bağlantı: A Hard Day’s Night: Solving a Beatles mystery with mathematics/
- A Hard Day’s Night by numbers: The Beatles decoded. Yaınlanma tarihi: 5 Temmuz 2012. Kaynak site: The Conversation. Bağlantı: A Hard Day’s Night by numbers: The Beatles decoded
Size Bir Mesajımız Var!
Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak veya Patreon üzerinden ufak bir bağış yaparak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel