Modern trigonometri anlayışımız, gök cisimlerinin gece gökyüzündeki hareketini inceleyen eski Yunan astronomlarına kadar uzanır. Ancak bu bilgimiz de yanıldığımızı 2017 yılında ortaya çıkan bir keşif ile öğrenmiş olduk. Anlaşılan Babilliler, Yunan astronomlarından yaklaşık 1000 yıl önce trigonometrinin öncülü kabul edeceğimiz bazı çalışmalar yapmışlardı. Üstelik bu çalışmalarını yaparken açılara da ihtiyaç duymamışlardı.

Günümüzde Irak’ın civarlarında, Babil’in kayıp şehirlerinden kalma, binlerce kil tablet çıkarıldı. Bu belgeler binlerce yıl boyunca çölün altında saklı kalmıştı. Ancak bir kez ortaya çıktıklarında müzelere, kütüphanelere ve özel koleksiyonlara girdiler. Bunlardan bir tanesi de Si.427 isimli 3700 yıllık bir tabletti.
Si.427 Tableti Matematik Tarihini Biçimlendirdi
Bu tablet, Bağdat’ın güneybatısındaki Sippar’da 1894’te bir arkeolojik keşif gezisi sırasında Jean-Vincent Scheil tarafından keşfedilmiştir. İşin ilginç tarafı Yeni Güney Galler Üniversitesi’nden matematikçi Dr. Daniel Mansfield onu fark edene dek bu tablet İstanbul Arkeoloji Müzesi’nde sergilenmiştir. ( Hala da orada sergilenmektedir.)

Günümüzde M.Ö 1900-1600 yıllarından kalma bu tablet, uygulamalı geometrinin bilinen en eski örneği olarak kabul ediliyor. Si.427, satılmakta olan bir arazi parçası ile ilgili. Çivi yazısıyla yazılan tablet, bataklık alanların yanı sıra bir harman yeri ve yakındaki bir kuleyi içeren bir alanı tanımlıyor.
Bunlar o döneme ait sıradan bilgiler gibi gelecektir. Oysa ki Si.427’de çok farklı bir şey var. Si.427 tabletinde üç Pisagor üçlüsünün kullanıldığı göze çarpıyor. Bu üçlüler, ( 3, 4, 5); (8, 15, 17); ve (5, 12, 13) üçlüleri.
Muhtemel lise yıllarından aklımızda en çok kalan Pisagor teoremidir. Bu teorem a2+ b2= c2 biçimindedir. Devamında öğretmenler öğrencilere, bazı sıralı üçlüleri ezberlemelerini öğütlerler. Bu sıralı üçlüler grubunun bazıları Pisagor Üçlüleri olarak bilinirler. Pisagor Üçlülerinin bazıları (3, 4, 5); (5, 12, 13); (8, 15, 17); (7, 24, 25); (20, 21, 29); (12, 35, 37); (9, 40, 41)… biçimindedir.
Pisagor üçlüleri, antik Hindistan’da, potansiyel olarak MÖ 800’e kadar uzanan dikdörtgen ateş sunakları yapmak için kullanıldı. Si.427 sayesinde artık eski Babillilerin bunlar arazi ölçümleri yapmak için kullandıklarını biliyoruz.
Aslında bu bilgileri ilk araştırma yayınlandığı zaman öğrenmiştik. Ancak matematikçi Dr. Daniel Mansfield bu bulgunun devamında araştırmalarına devam etti. Onu ilgilendiren şey Babilliler neden dik açılı üçgenlerle ilgilendikleri ve tam olarak nasıl kullandıkları idi.
Babilliler Bu Tabletleri Ne Amaçla Kullanmışlardı?
Babilliler, bugün bizim kadar toprağa değer veriyordu. Önceleri, geniş tarım arazileri tapınaklar veya saraylar gibi kurumlara aitti. Profesyonel eksperler, hasadın büyüklüğünü tahmin etmek için bu alanları ölçerlerdi. Arazi mülkiyetinin doğası, MÖ 1900 ile 1600 arasındaki Eski Babil döneminde değişti. Bu dönemde sıradan insanlarda topraklara sahip olabilmeye başlamıştı.
Bu değişikliğin arazinin ölçülme şekli üzerinde bir etkisi oldu. Kurumların aksine, özel arazi sahipleri, sınırları belirlemek ve anlaşmazlıkları çözmek için bilirkişilere ihtiyaç duyuyordu. Modern ölçüm araçlarının olmadığı bir dönemde de bu bilirkişiler ölçüm için dikdörtgen, dik açılı üçgen, dik yamuklar gibi şekilleri referans olarak kullanıyordu.
Ancak elinizde sadece bir ölçüm ipi ve birim çubuk olduğunu düşünün. Bir dik açıyı nasıl elde edersiniz? Cevap tabi ki Bir Pisagor üçlüsü yaparak biçiminde olacaktır. Tam da bu noktada bir başka Babil tableti hakkında bilgi sahibi olmanız gerekiyor.
Plimpton 322 Tableti

Babil matematiği bugün kullandığımız 10’luk tabanlı sayılar yerine 60’lık sayı tabanını kullanmıştı. (Saatleri ve açıları ölçerken 60 sayısını kullanmamızın nedeni Babillilerdir.) Bu sayede hesaplamada daha az yuvarlama var. Sonucunda 10’u bölen sadece iki sayı vardır. Bunlar 2 ve 5’tir. Ancak 60’ın çok daha fazla böleni vardır. (Tam olarak 12 tane.) Sonucunda bu da 60’lık sayı tabanını hesaplamalar için daha uygun hale getirir.
Plimpton 322, modern bir trigonometrik tabloya benzeyen Pisagor üçlülerinin bir listesini içeren bir başka antik Babil tabletidir. Aslına bakarsanız Mansfield bu tabloda yer alan Pisagor üçlüleri ile ilgili araştırmalar yaparken tesadüfen Si.427 Tabletini keşfetmiştir.
Plimpton 322 bize bir Pisagor üçlüsünün hangi kenarlarının düzenli olduğunu ve bu nedenle ölçmede yararlı olduğunu söyler. Bu tabletin yazarının gerçek niyetini asla bilemeyecek olsak da, bildiğimiz şey, Babillilerin Pisagor üçlüleri hakkında kendi benzersiz anlayışlarını geliştirdikleridir.
Babil Tabletleri Bu Uygarlığın Trigonometriyi Bilindiğin Dışından Tekniklerle Uyguladığını Gösteriyor.
Babillilerin modern açı kavramına ihtiyaç duymayan tamamen farklı bir trigonometri biçimi kullanmışlardı. Okulda bize dik açılı bir üçgenin şeklinin diğer iki açıya bağlı olduğu söylendi. Açı, 360 parçaya veya dereceye bölünmüş bir dairenin çevresi ile ilgiliydi.
Bu açı daha sonra dik açılı üçgenin kenarlarının sin, cos ve tan ile oranlarını tanımlamak için kullanılmaktaydı. Bu esnada da elbette elimizde aşağıda gördüğümüz gibi trigometrik oranları gösteren bir çizelge olması gerekliydi.
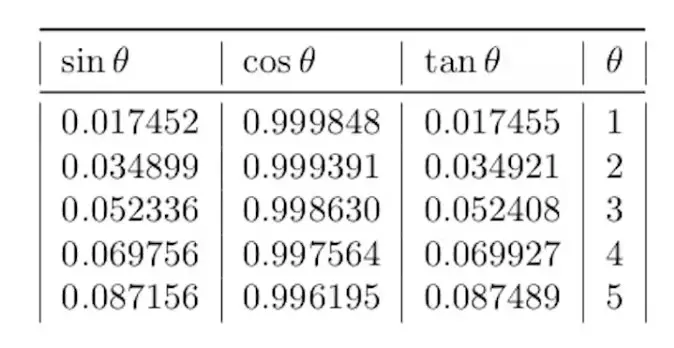
Bu yaklaşımın ilk izleri karşımıza M.Ö. 120’de yaşamış olan Yunan gökbilimci Hiparkus‘un çalışmalarında çıkar. Ay ve Güneş’in yörüngelerini hesaplamak için bu tarz bir tablo kullandığı için de kendisi trigonometrinin babası olarak anılmaktadır. Ancak Babilliler, çok daha önceleri kendi benzersiz trigonometri hesaplama yöntemlerini keşfetmişlerdi.
Babilliler, tamamen farklı bir dik üçgen kavramsallaştırmasına sahipti. Onu bir dikdörtgenin yarısı olarak gördüler ve 60 tabanlı sayı sistemleri sayesinde yalnızca tam oranları kullanarak çok çeşitli dik üçgenler elde ettiler. Aşağıdaki görselde solda günümüzde alışageldiğimiz trigonometrik gösterim biçimi var. Sağda ise Babil trigonometrisinin nasıl uygulandığını görüyorsunuz.
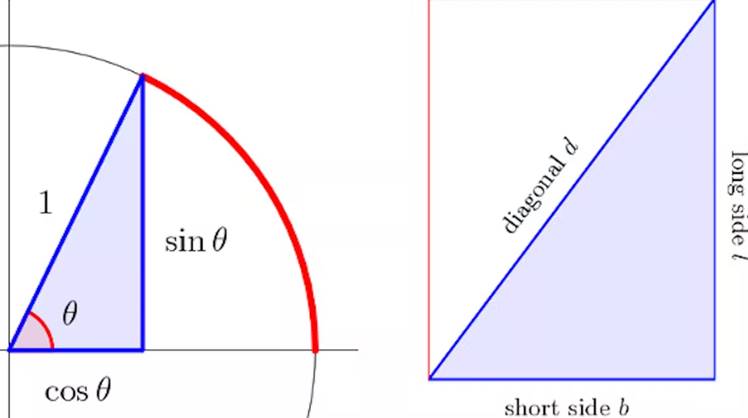
Bu hesaplamada sin ve cos’u bir kenara atıp bunun yerine b/l ve d/l oranlarına bakıyoruz. Tan yerine geçen oran o zaman b/d veya d/b olacaktır. Burada b, l ve d bir dikdörtgenin kısa kenarı, uzun kenarı ve köşegenidir.
Plimpton 322’nin hayatta kalan parçası Pisagor üçlüsü 119, 120, 169 ile başlar. Sonraki üçlü 3367, 3456, 4825’tir. Bu tabletin tamamı günümüze ulaşmamıştır. Ancak toplamda 38 satır içerdiği düşünülmektedir. Aşağıda bir kısmının günümüzdeki karşılıklarını görebilirsiniz.
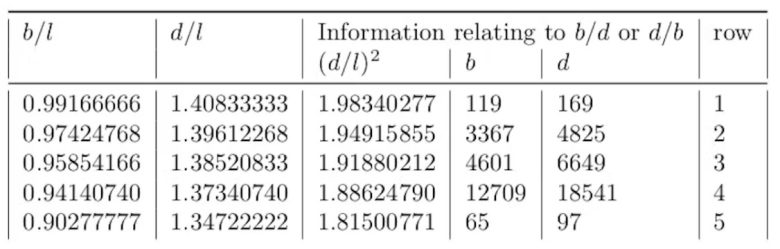
Şimdi son bir soru kaldı. Si.427 Tabletinde neden sadece 3 tane Pisagor üçlüsü vardı? Bir Pisagor üçlüsünü kullanışlı kılan kenarlarıdır. Bu sayede tam bir dik üçgen elde ettiğinizden emin olursunuz. Bu nedenle seçtiğiniz üçgenin 60 sayısını ve 60 sayısının katlarını bölen sayılar olması gereklidir. Si.427 Tabletindeki ilk üç Pisagor üçlüsünün kenarları bunu sağlamaktadır. ( Daha fazla bilgi için: Regular number)
Sonuç Olarak;
Kesin olan bir şey var ki, keşfedilmeyi bekleyen daha birçok sır barındıran, bu kadim uygarlığı anlamaya yeni başlıyoruz.
Kaynaklar ve ileri okumalar
- How ancient Babylonian land surveyors developed a unique form of trigonometry — 1,000 years before the Greeks. Yayınlanma tarihi: 4 Ağustos 2021; Bağlantı How ancient Babylonian land surveyors developed a unique form of trigonometry — 1,000 years before the Greeks./
- Mansfield, Daniel. (2021). Plimpton 322: A Study of Rectangles. Foundations of Science. 26. 10.1007/s10699-021-09806-0.
- Written in stone: the world’s first trigonometry revealed in an ancient Babylonian tablet. Yayınlanma tarihi: 24 Ağustos 2017; Bağlantı: Written in stone: the world’s first trigonometry revealed in an ancient Babylonian tablet.
Matematiksel








