Satranç oyunu üzerine kurulu en ilginç bulmacalardan biri matematikçi Euler’in çalışmalarının ardından popülerlik kazanmış At Turu problemidir.

Bir satranç seti alın ve bir at hariç taşların hepsini atın. At’ı satranç tahtasının 64 karesinden herhangi birine yerleştirin. Şimdi çözmeniz gereken problem şudur. Bu atı 64 adet kareye sadece 1 kez uğrayarak satranç tahtasında hareket ettirmeniz mümkün müdür?
At Turu Problemi İle İlgili Sorun Nedir?
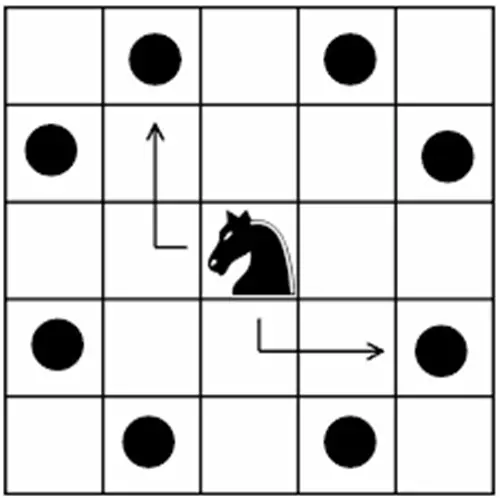
Hatırlatmak gerekirse, at satranç tahtasında L harfi şeklinde hareket eder (2 adım bir yöne, sonra 1 adım buna dik olacak yöne). Bu yüzden, boş bir satranç tahtasının ortasında bulunan bir at, aşağıda gördüğünüz 8 farklı hareketten birini yapacaktır.
At turu problemi başlangıçta kolay bir soru gibi gözükecektir. Ancak Euler bunu “herhangi bir analize tabi olmayan ilginç bir problem” olarak nitelendirmişti. Yine de analizi yaptı ve bunu sistemli bir şekilde yapan ilk kişi de aslında oydu. ( Bilinen en eski referans MS 9. yüzyıla kadar uzanmaktadır.)
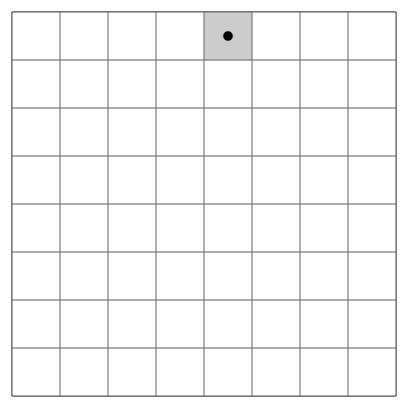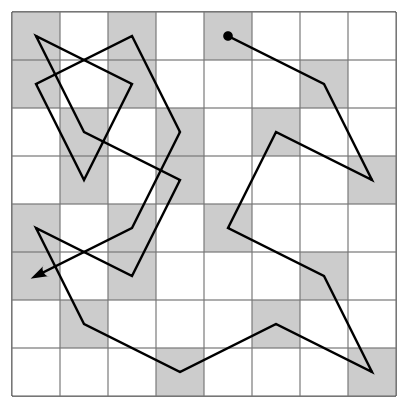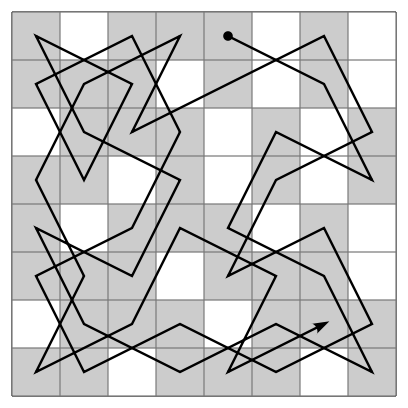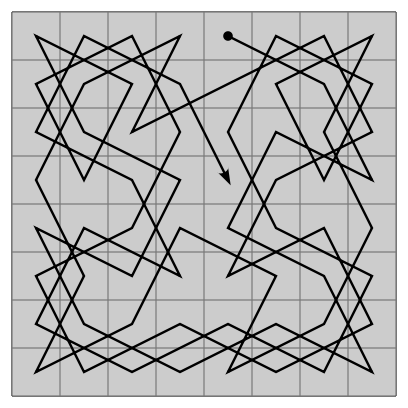
Onun çalışmalarından bir örneği aşağıda görüyorsunuz. ( Euler kareleri geçildikleri sıraya göre numaralandırmıştı. Mavi çizgiler sonradan eklenmiştir.)

Euler arşivinden (E309 isimli makale)
Tüm zamanların en önemli matematikçilerinden biri olsa da Euler’in at turu problemini deneme yanılma ile çözmesi imkansızdı. Çünkü asıl sorun bir tane bulmak değildi. Bu tip turlardan kaçının olası olduğunu hesaplamak istiyordu. Bunları gerçekten saymaya çalışmak için bir bilgisayar kullanmanız gerekir. 1996’da matematikçiler Martin Löbbing ve Ingo Wegener tam da bunu yaptı.
At turu probleminde 63 hamleyi yapar ve 64. hamleyle orijinal kareye geri dönebileceğiniz bir kareye ulaşırsanız, buna kapalı tur denir. Diğer turlara da açık tur denir. ( Kapalı turlara Hamilton yolu da denir. Çünkü at turu problemi, grafik teorisindeki Hamilton yolu probleminin bir örneğidir.)
Matematikçiler bitiş karesinin başlangıç karesinden sadece bir at sıçraması uzaklıkta olduğu turları, yani bir döngüye dönüştürülebilen turları saydılar. Bunlardan 33.439.123.484.294 tane olduğunu iddia ettiler. (Aslında amaçları tur sayısını saymak değil, belirli bir sayım yönteminin yararlılığını göstermekti).
Ancak kısa süre sonra sonucun doğru olmadığı ortaya çıkacaktır. Görünüşe göre doğru sonuç 26 trilyondan daha fazlaydı. Döngüye dönüştürülemeyen at turu sayıları için de 2014’te hesaplanan bir sayı 19.591.828.170.979.904 kadardı. Ancak kimse bunun doğru olup olmadığından tamamen emin değil. Sayının bundan çok daha fazla olması da olasıdır.
Karıncalar Bir Satranç Problemini Çözebilir mi?
Karıncaların günlük yaşamlarındaki etkileyici işbirliği ve iz bırakma yetenekleri, bilim dünyasında karmaşık optimizasyon problemlerine çözüm arayan araştırmacılar için büyük bir ilham kaynağıdır. Karınca koloni algoritması, bu doğal süreçlerden ilham alarak geliştirilen bir yapay zeka yaklaşımıdır. Özellikle, bir karınca kolonisinin yiyecek kaynaklarını bulma ve en kısa yolu keşfetme yeteneği, bu algoritmanın temelini oluşturur.
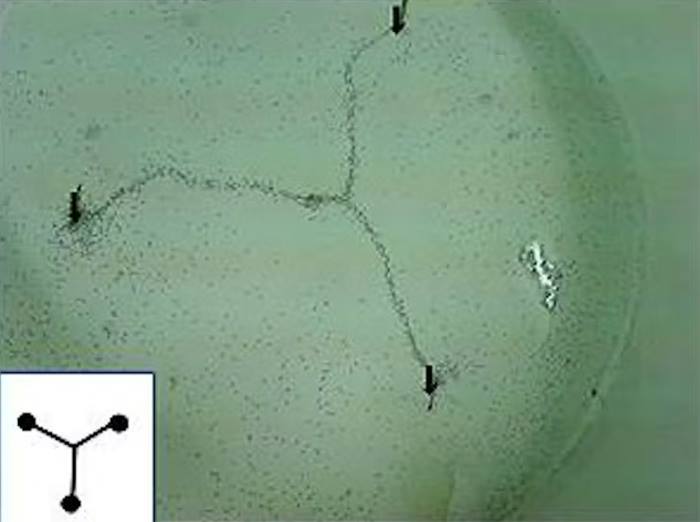
Bu algoritma, bir karınca kolonisindeki karıncaların davranışlarını ve etkileşimlerini taklit ederek çalışır. Karıncalar, yiyecek kaynaklarına ulaşmak için dolaşırken arkalarında feromon adı verilen çekici bir kimyasalın küçük damlacıklarını bırakırlar.
Diğer karıncalar ise bu kimyasalın cazibesine kapılır ve onu takip ederken kendi feromon damlacıklarını bırakarak ize eklenirler. Hansel ve Gretel’in ekmek kırıntılarından iz bırakması gibi, karıncalar da evlerine dönüş yolunu bulmak için bu izleri kullanırlar.
En başarılı karıncalar (sorunu daha iyi çözenler), kötü performans gösterenlerden daha fazla feromon bırakır. Bu süreç birçok kez (belki milyonlarca kez) tekrarlanır. Tekrarlar sayesinde, iyi çözümlerdeki feromon izleri artar ve buharlaşma nedeniyle daha zayıf çözümlerde azalır.
Karınca koloni algoritması da benzer bir şekilde, olası çözüm yollarını arayarak, daha iyi çözümlere ulaşmak için bir takım işaretler ve denemeler yoluyla yol haritası oluşturur. Bunun için elbette gerçek karıncalar değil karınca popülasyonunu simüle eden bir bilgisayar kullanılacaktır.
Geçtiğimiz yıllarda araştırmacılar at turu problemini çözmek için karınca kolonisi optimizasyon algoritmasını kullanmaya karar verdiler. Simülasyonda, karıncaların yalnızca satranç tahtasındaki bir at gibi hareket etmesine izin verildi. Ayrıca karıncalar satranç tahtasının sınırları içinde kalmak zorundaydı. Bu algoritmayı kullanarak araştırmacılar yaklaşık yarım milyon tur buldular.
Sonuç Olarak
Karınca algoritmasının neden bu kadar iyi performans gösterdiğini söylemek kolay değil. Belki de algoritmik parametreleri ayarlamaktan kaynaklanıyordu. Ya da belki de karıncalar gerçekten satranç oynamayı seviyordu!
At turu problemi çözümsüz bir satranç problemi değildir. Ancak kaba kuvvetle ( yani deneme yanılma ile) çözmek de olası değildir. Bilgisayar kullanarak belirli bir tahtada at turunu bulmanın birkaç yolu vardır. Konu ilginizi çektiyse sizin de bu algoritmalardan birini kullanarak denemeler yapmanız olasıdır. Daha fazlası için göz atınız.
Kaynaklar ve ileri okumalar
- How to get ants to solve a chess problem. Yayınlanma tarihi: 30 Ocak 2014. Kaynak site: Conversation. Bağlantı: How to get ants to solve a chess problem
- The knight’s tour. Kaynak site: Plus Math. Yayınlanma tarihi: 5 Ağustos 2016. Bağlantı: The knight’s tour
- Rezvanian, Alireza & Vahidipour, S Mehdi & Sadollah, Ali. (2023). An Overview of Ant Colony Optimization Algorithms for Dynamic Optimization Problems. 10.5772/intechopen.111839.
Size Bir Mesajımız Var!
Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel





