Bir çok kişiye matematik soğuk, soyut bir konu gibi görünür. Oysa ki bu tutkulu ve hayat dolu Evariste Galois bize başka bir matematikçi modeli sunar.

Évariste Galois’nin yalnızca yirmi yıl yaşamış olması, hikâyesinin kısa olacağını düşündürebilir. Ancak bu kısa ömrüne sığdırdığı çalkantılı olaylar ve bilimsel başarılar, onu tarihte özel bir yere taşır. Galois’nin adı bugün soyut cebirin önemli bir alanı olan “Galois Kuramı”yla birlikte anılmaktadır. Matematikte bir kurama adını verebilmek, nadir rastlanan bir onurdur.
Evariste Galois Ne Yaptı?
Galois Kuramı, grup kuramı ile alan kuramı arasında derin bir ilişki kurar. Bu açıklama, matematikle ilgilenmeyen biri için ilk etapta anlamsız görünebilir. Ancak bu kuramın sağladığı bazı temel sonuçlar oldukça dikkat çekicidir. Örneğin, yüksek dereceli denklemlerin sadece dört işlem ve kök alma yöntemleriyle çözülebilir olup olmadığını belirlemeye olanak tanır.
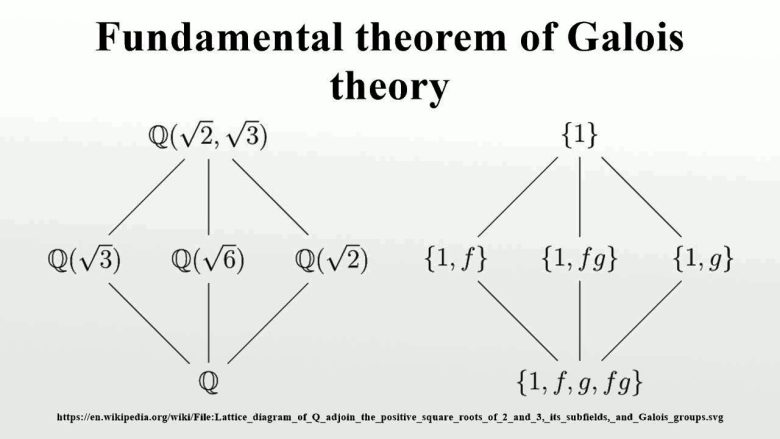
Galois’nin çalışmaları aynı zamanda yalnızca cetvel ve pergel kullanarak hangi düzgün çokgenlerin çizilebileceğini açıklar. Bununla birlikte, neden genel bir açının bu araçlarla üçe ayrılamayacağını da ortaya koyar. Lisede karşılaşmış olabileceğiniz bu basit görünen problemler, aslında Galois’nin devrim niteliğindeki fikirleri sayesinde açıklığa kavuşmuştur.
Onun ortaya koyduğu, permütasyonlardan oluşan gruplar fikri, grup kuramına atılan ilk büyük adımlardan biriydi. Bu kuram, zamanla matematiksel simetrinin temel yapı taşına dönüştü ve günümüzde hâlâ aktif bir araştırma alanı olarak varlığını sürdürüyor. Peki aşk bunun neresinde? Sanırız hikayeyi baştan anlatmalıyız.
Kısaca Evariste Galois Kimdir?
Évariste, 1811 yılında, Büyük Fransız İhtilali’nin etkisinin sürdüğü ve Fransa’nın Napolyon yenilgisiyle sarsıldığı bir dönemde dünyaya geldi. Ailesi varlıklı ve nüfuz sahibiydi; siyaset aile geleneğiydi. Babası Nicolas-Gabriel Galois, Paris yakınlarındaki Bourg-la-Reine kasabasının belediye başkanıydı.

Klasik eğitim almış olan annesi Adelaide-Marie Demante, Évariste’in eğitimine erken yaşta evde başladı. Çocuk, on iki yaşında okula başladığında, devrimci karakteri, siyasal çalkantılar içindeki Fransa’da kendini göstermeye başladı.
Henüz on dört yaşındayken, Legendre’ın Éléments de Géométrie adlı eserini bir roman okur gibi okuyup kısa sürede bu alanda derinleştiği söylenir. Aynı yıl, kendi başına birçok önemli matematiksel çalışmayı okuyup tamamladığı bilinmektedir.
Galois, matematik öğretmeninin uyarılarını dikkate almadan, prestijli École Polytechnique’e bir yıl erken başvurdu ve sınav için herhangi bir hazırlık yapmadı. Sonuç olarak sınavı geçemedi. 1829’da, denklem kuramı üzerine yazdığı bir makaleyi Paris Bilimler Akademisi’ne gönderdi, ancak bu çalışma kayboldu.
Galois, bu durumu yeteneğinin kasten görmezden gelinmesi olarak yorumladı. Aynı yıl, hayatında başka ağır darbeler yaşadı. Babası, köy papazıyla yaşadığı siyasi bir çatışma sırasında, papazın kötü niyetli belgelerde onun imzasını taklit etmesi üzerine intihar etti. Kısa süre sonra Galois, École Polytechnique’e ikinci ve son kez başvurdu; ancak bu girişimi de başarısız oldu.
Bunun yerine, daha az saygın kabul edilen École Préparatoire’a (daha sonra École Normale) kabul edildi. 1829 yılı sonunda, hem fen hem de edebiyat alanında mezuniyetini tamamladı. Birkaç ay sonra, denklem kuramı üzerine hazırladığı çalışmanın yeni bir versiyonunu akademinin büyük ödülü için tekrar sundu.
Eğer gerçekten Galois’nın hayatını anlamak istiyorsak onun hayatının temel özetinin şanssızlık olduğunu anlamalıyız. Çünkü dönemin akademi sekreteri Fourier, el yazmasını eve götürdü ve raporunu hazırlayamadan hayatını kaybetti. Böylece çalışma bir kez daha kayboldu.
Galois, bu ikinci kaybı da bir komplo olarak gördü ve hak ettiği değerin kasıtlı olarak elinden alındığına inandı. Bu düşünce, Cumhuriyetçi görüşleriyle örtüşüyor ve onu devrim fikrine daha da yakınlaştırıyordu.
Evariste Galois romantik bir devrimci idi
Charles X, iktidarını kaybetme riskiyle karşı karşıyaydı. Bu tehlikeyi önlemek için basına sansür getirdi. Halk bu kararı protesto ederek ayaklandı. Bu gelişmeler sırasında, École Normale müdürü öğrencileri okul binasında kilitli tuttu. Bu karar, devrimci görüşleriyle tanınan Galois’yi öfkelendirdi.
Galois, Gazette des Écoles gazetesine müdüre yönelik sert eleştiriler içeren bir mektup gönderdi. Mektubunu imzasıyla yazmıştı; ancak gazete editörü adını yayımlamadı. Müdür, bu durumu fırsat bilerek Galois’yi, isimsiz mektup yazdığı gerekçesiyle okuldan uzaklaştırdı.
Galois, yaşananların ardından Cumhuriyetçi görüşlerin yoğunlukta olduğu Ulusal Muhafız Topçusu’na katıldı. Ancak bu birlik, kısa süre sonra kral tarafından güvenlik tehdidi olarak değerlendirilip lağvedildi.
Ocak 1831’de Galois, denklem kuramı üzerine hazırladığı üçüncü çalışmasını Fransız Bilimler Akademisi’ne sundu. Ancak iki ay boyunca herhangi bir yanıt alamadı. Bu durum karşısında, akademi başkanına bir mektup yazarak gecikmenin nedenini sordu. Yine de bir cevap verilmedi.
Temmuz ayında akademi, Galois’nin çalışması hakkında kararını açıkladı: “Galois’nin ispatını anlamak için her türlü çabayı gösterdik. Ancak gerekçeleri yeterince açık ve ayrıntılı değil; bu nedenle doğruluğunu değerlendiremiyoruz.”
Bu yanıt karşısında Galois öfkesine hâkim olamadı. Bastille Günü’nde, Cumhuriyetçi bir gösteride en ön safta yer aldı. Üzerinde Topçu birliğine ait üniforması ve silah vardı. Ancak bu iki durum da yasadışıydı.
Galois, tutuklandı ve altı aylık hapis cezasına çarptırıldı. Bu süreyi matematik çalışarak geçirdi. 1832 yılında kolera salgını başlayınca hastaneye sevk edildi ve ardından şartlı tahliye ile serbest bırakıldı.
Galois’nin yaşamındaki son döneme aşk damgasını vurdu. Hapisten çıktıktan sonra tedavi gördüğü merkezde, hekimin kızı Stéphanie’ye âşık oldu. Ancak ne yazık ki nişanlıydı.

Galois bu durumu önemsemedi ve duygularını açıkça dile getirdi. Onu bekleyen şey bir düello olacaktı. Rakibi, Galois’ye 25 adım mesafeden ateş etti. Kurşun karın bölgesine isabet etti. 21 yaşındaki genç adam matematikte bir devrim yaptığı gecenin sabahında hayatını kaybetti.
Evariste Galois’in Son Gecesi
Düellodan bir gün önce Galois, keşiflerini özetleyen bir mektubu Chevalier’e gönderdi. Bu mektupta, grup kavramının bir polinom denkleminin köklerle çözülebilir olup olmadığını nasıl belirlediğini anlattı. Ayrıca eliptik fonksiyonlar, cebirsel fonksiyonların integrasyonu ve anlamı hâlâ tam çözülemeyen bazı ipuçlarına da değindi. Mektubunu şu sözlerle bitirdi:
“Jacobi ya da Gauss’tan, bu teoremlerin doğruluğu hakkında değil, önemi hakkında kamuoyuna açık bir değerlendirme yapmalarını isteyin. Umarım bir gün, bu karmaşayı çözmek isteyen insanlar çıkar.”

Galois’nın ölümünden 10 yıl sonra Akademi Galois’nın çalışmasını onaylar. Ve genç adam makus talihine karşı verdiği amansız savaşta yüreğindeki tüm aşkı; bilme aşkını, sevme aşkını, devrim aşkını birbiriyle çarpar ve sonsuzluğa, kendi sonsuzluğuna ulaşır.
Neyse ki, matematik adına bu çağrıya kulak verenler oldu. Galois’nin çalışmalarını ilk fark eden kişi Joseph-Louis Liouville’di. Kısa süre sonra Jacobi de Galois’nin yazılarını inceledi ve onların değerini kavradı.
1909 yılında, École Normale müdürü şunları söyledi: “Bu okula isteksizce gelen, burada yanlış anlaşılan ve uzaklaştırılan ama sonunda okulun en parlak isimlerinden biri olan Galois’nin dehası adına özür dileme fırsatını verdiğiniz için teşekkür ederim.”
Peki, Galois matematik için ne yaptı?
Kısa cevap şu: Simetri kavramının temelini açıklığa kavuşturdu. Bu, bugün “grup” olarak bildiğimiz yapıdır. Simetri, artık matematik ve fizik dünyasının merkezinde yer alıyor. Hayvan desenlerinden moleküllerin titreşimine, salyangoz kabuklarının biçiminden temel parçacıkların kuantum mekaniğine kadar birçok alandaki anlayışımıza yön veriyor.
Kaynaklar ve ileri okumalar için:
- Genius, stupidity and genius again; Yayınlanma tarihi: 1 Mayıs 2005. Kaynak site: Plus Math. Bağlantı: Genius, stupidity and genius again
Matematiksel





