Arşimet’in adını kaldıraçlar, makaralar, gemi batıran düzenekler ve Arşimet vidasıyla duymuş olabilirsin. Ama o sadece mekanik aletlerle değil, çemberler ve küreler gibi geometrik şekillerle de derinlemesine ilgilenmişti. Aslında Arşimet, pi sayısı üzerine ilk ciddi çalışmaları yapan kişiydi ve bunu yaptığı sırada, daha sıfır sayısı bile matematikte yerini almamıştı.

Bu konuda elimizdeki ilk somut kayıt, onun Dairenin Ölçümü adlı eserinde yer alır. Bu önemli kitap, pi sayısının tarihsel gelişiminde dönüm noktası sayılır. Kitapta, daireyle ilgili üç temel önerme bulunur ve bu önermeler pi’nin anlaşılmasında büyük rol oynamıştır. Şimdi bu üç önermeyi, kısa açıklamalarıyla birlikte inceleyelim.
1.“Bir dairenin alanı, dik kenarları sırasıyla dairenin yarıçapı ve çevresine eşit olan bir dik üçgenin alanına eşittir.”

Yani Arşimet, dairenin alanını şöyle tanımlar: yarıçap ile çevreyi çarpıp ikiye böleriz. Bu, aslında dik üçgenin alan formülüne çok benzer: taban çarpı yükseklik, bölü iki.
Burada taban, dairenin çevresi; yükseklik ise yarıçapıdır. Arşimet’in bu yaklaşımı, daireyi çok sayıda ince dilime ayırıp onları uzun, dar bir üçgen gibi düşünerek geliştirdiği bir yöntemdir.
2. “Bir dairenin alanının, bir kenarı dairenin çapına eşit olan bir karenin alanına oranı 11:14’e yakındır.”
Arşimet’in ikinci önermesi budur. Şimdi bu oranı birlikte inceleyelim. Bir dairenin alanı πr2şeklindedir. Bir kenarı dairenin çapı, yani 2r olan bir karenin alanı ise (2r)2 = 4r2 olur. Bu iki alanı birbirine oranladığımız zaman sadeleştirmelerden sonra elimizde π/4 kalır. Arşimet, bu oranın yaklaşık olarak 11:14 olduğunu söyler. Yani:
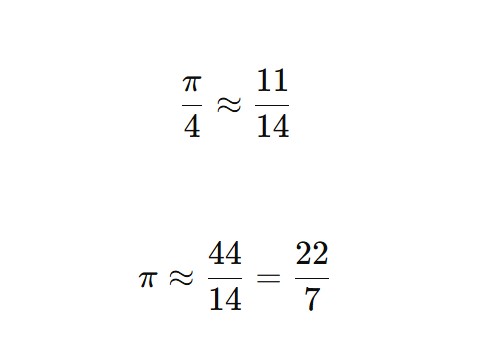
Sonuç olarak, Arşimet’in bu oran üzerinden yaptığı hesaplama, bugün hala yaygın şekilde kullanılan ve pi’nin en bilinen yaklaşık değeri olan 22/7’yi verir.
3. “Herhangi bir dairenin çevresinin çapına oranı 22/7 ile 223/71 arasındadır.” Şimdi kendisinin bu fikri nasıl elde ettiğine biraz daha yakından bakalım.
Arşimet’in Yaklaşım Yöntemi
Arşimet, dairelerin çevresini ve alanını yaklaşık olarak bulmak için çokgenlerden yararlandı. Dairenin içine ve dışına birer düzgün çokgen çizerek, dairenin çapının bu çokgenlerin çevrelerine oranını hesapladı. Dıştaki çokgenin çevresi daireninkinden daha büyük, içtekininki ise daha küçüktü. Bu durumda, dairenin gerçek çevresi bu iki değer arasında bir yerde olmalıydı.
Arşimet işe, en basit şekillerden biri olan düzgün altıgen ile başladı. Önce çapı 1 birim olan bir daire çizdi. Daha sonra köşeleri daireye değen bir iç altıgen, ardından kenarları daireye teğet olan biraz daha büyük bir dış altıgen çizdi.

Tanım gereği, bu dairenin çevresi pi sayısı kadar olacaktı. Arşimet, bu yöntemle daireyi bir alt sınır (iç altıgenin çevresi) ve bir üst sınır (dış altıgenin çevresi) arasına yerleştirmeyi başardı.
Arşimet, çokgenlerin kenar sayısı arttıkça şeklin daireye giderek daha çok benzediğini fark etmişti. Bu yüzden her adımda kenarları ikiye bölerek daireye daha yakın yeni çokgenler oluşturdu. Aynı yöntemi sırasıyla 12 kenarlı, 24 kenarlı, 48 kenarlı ve son olarak 96 kenarlı düzgün çokgenlerle uyguladı.
Sonunda Arşimet, pi sayısının 223/71’ten büyük, ancak 22/7’den küçük olması gerektiği sonucuna vardı. İlginçtir ki, bugün bildiğimiz pi değeri gerçekten de bu iki kesir arasında yer alır.
Arşimet’in Pi Sayısı Hesaplamasının Detaylarına Bir Göz Atalım
Arşimet’in yaşadığı dönemi düşündüğümüzde, tüm bu pi hesaplamalarını tamamen elle yaptığını unutmamak gerekir. Üstelik çokgenin kenar sayısı arttıkça bu işlemlerin ne kadar zorlaştığını tahmin etmek zor değildir. Peki bunu nasıl başardı?
Cevap trigonometri. Şimdi konuyu basit tutalım ve yeniden altıgenimize dönelim. Dairenin çapı 1 birimdi. Düzgün altıgenin, altı tane eşkenar üçgenin birleşiminden oluştuğunu biliyoruz. Bu durumda merkezdeki AOB açısı, 360 derecenin altıda biri olacağı için 60° olur. Ayrıca OK doğru parçası AB kenarına diktir. Bu yüzden AK ve KB uzunlukları eşittir; her birine a diyelim.

Şimdi AOK üçgeninde trigonometriyi kullanalım. Bu durumda sin30 = a / (1/2) = 2a olur. sin30’un 1/2 olduğunu bildiğimize göre 1/2 = 2a, buradan da a = 1/4 sonucuna ulaşırız. Altıgenin çevresi 12a olduğuna göre, çevre 3 birim çıkar.
Şimdi bu sonucu n kenarlı bir düzgün çokgen için genelleştirelim. Şekil her durumda düzgün olduğundan, aradığımız x açısının 360/n tepe açısının yarısı olduğunu biliyoruz. Biraz önce kullandığımız mantıkla, sin(180/n) = 2a olur. Dolayısıyla çokgenin çevresi, n tane 2a kadar olacaktır. Yani çevreyi n × sin(180/n) şeklinde ifade edebiliriz.
Bundan sonra yapmamız gereken, n yerine farklı değerler vererek çevrenin nasıl değiştiğini görmek. Aşağıda, n için bazı değerler seçtiğimizde elde edilen sonuçları görebilirsiniz.

Sonuç Olarak
Arşimet pi sayısını hesaplamak için şaşırtıcı bir öngörü ile doğru sonuca ulaşmıştı. Yöntemi o kadar sağlamdı ki sonraki beş yüz yıl boyunca kimse daha yakın bir sonuç elde edemedi.
Kaynaklar ve ileri okumalar
- The beautifully simple method Archimedes used to find the first digits of pi; Yayınlanma tarihi: 15 mart 2019; Bağlantı: https://www.businessinsider.com/
- King, Alessandra. (2013). Finding Pi with Archimedes’s Exhaustion Method. Mathematics Teaching in the Middle School. 19. 116-123. 10.5951/mathteacmiddscho.19.2.0116.
Matematiksel





