Aristoteles'in Çember Paradoksu Nedir?

Aristoteles’in çember paradoksu hem matematiğin hem de fiziğin nasıl iç içe geçtiğini ve sezgimizin nasıl kolayca yanılabildiğini gözler önüne serer.

Platon’un öğrencisi ve Büyük İskender’in öğretmeni olan Aristoteles (MÖ 384–322) gibi insanlar sık ortaya çıkmaz. Bugün çoğu kişi onu çıkarımsal mantığı sistemleştirdiği için bir matematikçi olarak görür, ancak onun fizik dünyasına yaptığı katkılar da çok büyüktür.

Aristotelesin Çember Paradoksu ‘nun kökeni Aristotelesin temel eseri Mechanica ya dayanır. Bu ilginç sorun yalnızca matematiği değil, fiziksel düşünceyi de içine alır.

Temelde tüm çemberlerin aynı çevreye sahip olması gerektiğini gösteren bu paradoks bize önemli bir matematiksel argüman vermektedir. Bu argümanı yeniden yapılandırmak, matematikçileri çok uzun bir süre rahatsız eden garip bir gerçek sayı özelliğini ortaya çıkarmıştır.

Bu sorun Aristotelesçi külliyatın bir parçasıdır ve Mechanica adıyla bilinen kısa derlemede yer alır. Bu derleme, mekaniğe ilişkin çeşitli matematiksel ve felsefi problemler içerir ve geleneksel olarak Aristotelese atfedilir.

Çember Paradoksu Nedir?

Bu paradoksu incelememiz için önce büyük çember, sonra o büyük çemberin içine bir de küçük çember çizmemiz gerekecektir. Paradoks şu biçimdedir.

Tekerleği kaymadan A Noktasından B Noktasına doğru tam bir tur yuvarladığımızı düşünelim. Büyük tekerleğin alt noktasının izlediği yol A ile B arasındaki düz çizgidir. Küçük tekerleğin alt noktasının izlediği yol ise C ile D arasındaki düz çizgidir. Bu iki çizgi aynı uzunluktadır. Bu sonuç iki tekerleğin çevresinin eşit olduğu izlenimini verir. Oysa çevreleri açıkça eşit değildir. Paradoks tam da burada ortaya çıkar.

Aristo’nun Çember Paradoksunda tekerlek A noktasından B noktasına bir tam tur (kaymadan) yuvarlanır. Sonuçta ikisi de aynı yolu almış gibi gözükecektir. Bu da iki tekerleğin de aynı çevreye sahip olduğu anlamına gelir ki açıkçası öyle değildir.

Ancak içteki küçük tekerleğin çevresinin büyük tekerleğin çevresinden daha az olduğunu biliyoruz. Ancak aldıkları yola dikkat ederseniz, A′B′ uzunluğu ile AB uzunluğu birbirine eşittir. Bu durumda küçük çemberin çevresiyle büyük çemberin çevresi birbirine eşit olmalıdır.

. Bu paradoksun ilginç yanı hem matematiksel hem de fiziksel bir açıklamasının bulunmasıdır. Paradoksu çözmeden önce biraz düşünmenizi isteriz.

Yukarıdaki animasyonda görüldüğü gibi, ortak merkezli iki tekerlek bir tam tur döndürüldüğünde tekerleklerin aldığı mesafeler birbirine eşit olur.

Çember Paradoksunun Çözümü Nedir?

Bu paradokstaki hata iki kaynaktan gelir. İçinde matematik olsa da sorun aslında fiziksel bir sorundur. Büyük çember A Noktasından B Noktasına kaymadan ilerler. Ama küçük çemberin C Noktasından D Noktasına aynı şekilde kaymadan gideceğini varsaymak yanlıştır. Küçük çember kayar. Küçük çemberin kaymasını engellemek için dişli bir düzenek ekleseydiniz bu kez hiçbir şey hareket etmezdi.

Her iki çemberin de kaymadan hareket etmesi fiziksel olarak mümkün değildir. Bu size önce tuhaf gelebilir. Bunu anlamanın kolay bir yolu vardır.

Büyük çemberi dünya büyüklüğünde, küçük çemberi ise yalnızca bir ayak yarıçapında düşünün. Bu ölçüler gözünüzde canlandığında hareketin kaymadan gerçekleşemeyeceğini sezmek çok daha kolay olur.

Matematiksel olarak bu paradoksa inanırsanız şunu da kabul etmiş olursunuz. Birbiriyle bire bir eşleştirilebilen iki doğru, Şekildeki AB ve CD doğruları gibi, aynı uzunluğa sahiptir. Oysa bunun doğru olmadığını açıkça biliriz.

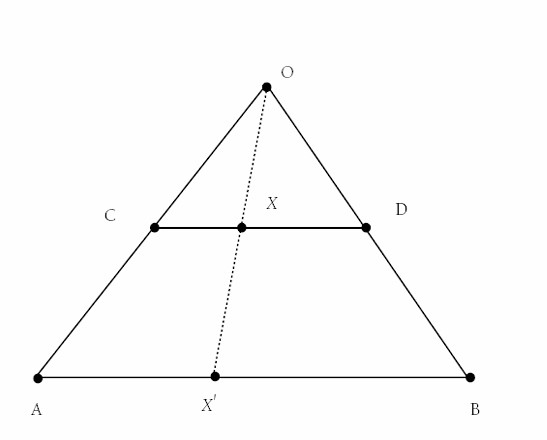
Farklı uzunluktaki çizgiler arasında bire bir eşleme yapmak olasıdır.

Farklı uzunluktaki doğrular arasında bire bir eşleme fikri kulağa tuhaf gelir. Çünkü sezgimiz uzunlukları farklı olan iki çizginin noktalarının da aynı sayıda olamayacağını söyler. Oysa matematik bu sezgiyi bozar.

Uzunluğu ne kadar olursa olsun her doğru parçası sonsuz sayıda noktaya sahiptir. Bu yüzden iki doğru parçası farklı uzunluklara sahip olsa bile noktaları arasında bire bir eşleme kurulabilir. Yani aynı sayıda noktaya sahip olmak aynı uzunlukta olmak anlamına gelmez.

Sonuç olarak

Aristoteles’in çember paradoksunda yaşanan matematiksel yanılgı tam olarak budur. Doğruların bire bir eşlenebilmesi onların eşit uzunlukta olduğunu göstermez. okta sayısı sonsuzdur ve uzunluk kavramı bu eşleme ile değişmez.

Okumak İsterseniz: Matematikçiler Onlarca Yıllık Geometri Problemini Çözmek İçin Tekerleği Daha Yüksek Boyutlarda Yeniden İcat Ediyor

Kaynaklar ve ileri okumalar için:

Gal, Ofer & Chen-Morris, Raz. (2012). Nature’s drawing: Problems and resolutions in the mathematization of motion. Synthese. 185. 10.1007/s11229-011-9978-5.
Lopes, Renato & Ferigolo, Jorge. (2024). Taphonomic significance of Aristotle’s ‘Wheel Paradox. An example with the cerithid gastropod Cerithium atratum (Born, 1778) from Conceição Lagoon. Santa Catarina State, Southern Brazil. Revista Brasileira de Paleontologia. 26. 272-287. 10.4072/rbp.2023.4.03.
Xu, Huiling & Yan, Xun-Wang & Wang, Yanyun. (2022). Understanding Aristotle’s Wheel Paradox from the Viewpoint of Motion Decomposition. The Physics Teacher. 60. 212-214. 10.1119/5.0055440.
Aristotle’s Wheel Paradox – To Infinity and Beyond. Kaynak site : Youtube. Bağlantı: Aristotle’s Wheel Paradox – To Infinity and Beyond

Size Bir Mesajımız Var!

Matematiksel, matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.

Matematiksel

Etiketler