Yunan matematiği Öklid’den sonra da gelişimini sürdürdü. Pergeli Apollonios Yunan matematiğinin altın çağının belki de son büyük matematikçisiydi. Bu nedenle adı günümüzde o dönemin en iyilerini temsil eden Arşimet ve Öklid ile beraber anılmalıdır.
(Pergeli Apollonius, isim benzerliğinden dolayı aynı dönemlerde yaşamış Rodoslu Apollonios ile karıştırılmaktadır. Rodoslu Apollonios şair ve İskenderiye Kütüphanesinin yöneticisidir. Bu isim karışıklığını engellemek için yaşadıkları yer isimlerinin önüne genelde eklenmektedir.)
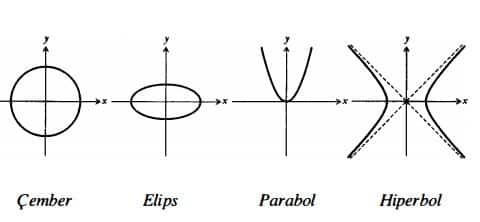
Konikler ile ilgili kitabında parabol, elips ve hiperbol gibi terimleri ilk o tanıtmıştır. Ancak bu bilginin değeri ve önemi Rönesans Dönemine kadar fazla anlaşılmamıştır. Çalışmaları 1605 yılında Kepler’in dikkatini çekmiş ve sonucunda onun gezegenlerin hareketleriyle ilgili ünlü çalışmasına ilham vermiştir.
Kısaca Pergeli Apollonius
Apollonius, Bugün Antalya il sınırları içinde bulunan Pamfilya bölgesindeki Perge kentinde dünyaya gelmiştir. Çağındaki tüm bilginler gibi İskenderiye kentine gitmiş, Öklid’den sonra gelen matematikçilerden dersler alarak kendisini geliştirmiştir. Devamında da günümüzde İzmir ilimize bağlı bulunan, dönemin önemli bir bilim merkezi olan Bergama’ya geçmiştir.
Burada bir süre çalışmış, dersler vermiş fakat en önemli işi belki de insanlık tarihini etkileyecek Konikler adlı ünlü yapıtını yazmak olmuştur. Apollonius’un hayatıyla ilgili bilgiler ne yazık ki günümüze fazla ulaşmamıştır. Bildiklerimiz kitaplarının önsözlerine kendisi ile ilgili yazdıkları ile sınırlıdır.
Apollonius ve Konikler

Arşimet’in fikirlerini geliştiren Apollonius’un en ünlü eseri olan Konikler, MÖ 2. yüzyılın başlarında bitmiştir. Kitap içerisinde 487 teorem barındırmakta ve sekiz ciltten oluşmaktadır. Apollonius, eserin ilk dört cildinde, kendisinden önceki matematikçilerin çalışmalarının bir derlemesini yapmıştır. Diğer dört ciltte ise yeni ve özgün olan kendi çalışmalarını yazmıştır.
Kitabında Apollonius ilk ilkelerden yola çıkarak bu eğrilerin geometrik özelliklerini sistematik bir şekilde inceler. Apollonios koni kesitlerini, bir çift dairesel koni ile bir düzlemin kesişim eğrileri olarak tanımlamıştır.
Düzlem koninin ana eksenine dik olursa kesişim eğrisi bir dairedir. Düzlemin eğiklik derecesi değiştikçe eğri daireden, önce elipse, sonra parabole, en sonunda da iki parçalı hiperbole dönüşür. Apollonios koni kesitlerinin analitik yoldan da tanımlanabileceğini göstermiştir. Özellikle de elipsin odak noktalarını tanımlaması önemlidir.
Apollonios Problemi
Geometri problemleri içerisinde en uğraştırıcı olanlarından biri olarak kabul edilen, üç çembere teğet olma koşulunu yerine getirecek bir çemberin çizimi “Apollonios Problemi“ olarak bilinir. Problemin genel çözümü ise çok sonraları ünlü matematikçi Gauss tarafından gerçekleştirilmiştir.

Sekiz ciltlik Konikler eserinden başka pek çok eser yazmış olan Apollonios’un ne yazık ki bu eserlerinin hiçbiri günümüze ulaşamamıştır. Ancak diğer yazarların aktardığına göre kendisinin irrasyonel sayılar hakkında çalışmalar yaptığı ayrıca pi sayısının hesaplanması için Arşimet’ten daha kesin bir yöntem bulduğu bilinmektedir.
Apollonius ayrıca astronomi ile de ilgili önemli çalışmaları vardır. Syntaxis adlı kitabında Ptolemy, Apollonius’un gezegenlerin gökyüzündeki hareketini açıklamak için eksantrik ve episiklik hareket sistemleri sunduğunu söyler.
Apollonius’un Yeniden Keşfi

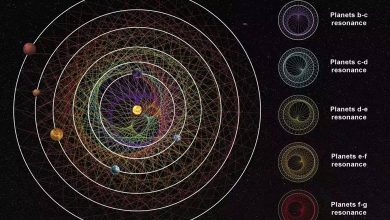
16.yüzyılın sonlarında ve 17. yüzyılın başlarında, Avrupa’da Apollonius’un Koniklerinin birkaç tercümesi ortaya çıktı. Devamında çalışmaları dönemin ünlü matematikçilerinin dikkatini çekti. Apollonius’a ait parabol ve elips kavramlarına başvuran Kepler “Bütün gezegenler odaklarından birinde Güneş’in bulunduğu elips biçimli yörüngeler üzerinde hareket ederler,” ifadesiyle “Kepler Yasası” adıyla bilinen yasayı oluşturdu.
Eğer Apollonius’un çalışmaları gerekli altyapıyı oluşturmasaydı, belki de Kopernik, Kepler ve Galileo keşiflerini gerçekleştiremeyecek hatta Newton yerçekimi yasasını hiç bulamayacaktı. Bilime olan büyük katkılarından dolayı Apollonius’un adı Ay üzerindeki bir kritere verilerek ölümsüzleştirmiştir.
Kaynaklar ve ileri okumalar:
- Apollonius of Perga; https://mathshistory.st-andrews.ac.uk/
- A to Z of mathematicians / Tucker McElroy.
Matematiksel