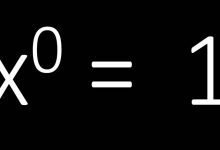1978’de Fransa’nın Marsilya kentinde düzenlenen büyük bir matematik konferansının organizatörleri, programa son dakika bir ekleme yapılacağını duyurdular. Öğle yemeği sırasında matematikçi Roger Apéry, matematikteki en ünlü sayılardan birinin iki tam sayının oranı olarak ifade edilemeyeceğinin kanıtını sunacaktı. ζ(3)’ün (Apéry sabiti) irrasyonelliğini kanıtlaması, matematik dünyasında büyük bir şaşkınlık ve heyecan yaratmıştı.

Konferans katılımcıları şüpheciydi. Matematikçiler yüzyıllardır ζ(3)‘ün irrasyonelliğini kanıtlamaya çalışıyordu. Dönemin en parlak matematikçilerinden biri olan İsviçreli Leonhard Euler, bu problemi çözmeye çalışmış ancak başarısız olmuştu. Şimdi ise, 60’lı yaşlarında ve pek tanınmayan bir Fransız matematikçi olan Apéry, bu yüzyıllık bilmeceyi çözdüğünü iddia ediyordu.
Ders hızla bir kaosa dönüştü. Apéry, çok az açıklama yaparak, denklem üstüne denklem sundu. Konuşmasını Fransızca yaptı, zaman zaman şakalar yaptı ve ispatın temel unsurlarına dair kritik açıklamaları atladı.
Örneğin, konuşmasının başında tahtaya kimsenin daha önce görmediği ama ispatının temelini oluşturan bir denklem yazdı. Salondakiler bu denklemin nereden geldiğini sorduğunda, Apéry’nin “Bahçemde yetişiyorlar” diye cevap verdi. Bu yanıt, salondaki birçok matematikçinin yerinden kalkıp salonu terk etmesine neden oldu.

Ancak en az bir kişi konuşmadan Apéry’nin haklı olduğuna ikna olmuş bir şekilde çıktı. Henri Cohen, argümanının temel fikrini anladı ve hemen çalışmaya koyuldu. Birkaç ay içinde, bir grup matematikçiyle birlikte kanıtın eksik noktalarını tamamladı. Yaklaşık iki ay sonra, Apéry’nin gerçekten Euler’in 200 yıl önce başaramadığını başardığı ortaya çıktı. Apéry, ζ(3)’ün irrasyonel bir sayı olduğunu göstermeyi başarmıştı.
Matematikçilerin sayılarla ilgili böylesine temel bir soruyla hâlâ boğuşuyor olmaları şaşırtıcı görünecektir. Ancak rasyonellik temel bir kavram olsa da araştırmacıların belirli bir sayının irrasyonel olduğunu kanıtlamak için çok az araçları vardır. Ve sıklıkla bu araçlar başarısız olur.
Zeta Fonksiyonu Nedir?
1644 yılında, İtalyan matematikçi Pietro Mengoli, tüm kare sayıların terslerini toplarsak ne olacağını merak etti. Ancak, bu toplamın sonucunu hesaplamayı başaramadı. Sadece Mengoli değil, dönemin birçok matematikçisi de bu problemi çözemedi. Bu başarısızlıklar arasında, İsviçre’nin Basel kentinde yaşayan ünlü Bernoulli ailesinden bilim insanları da vardı.
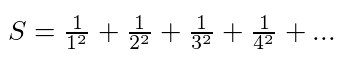
Aslında, bu sorunun çözülmesi 90 yıl daha sürdü. Sonunda, yine Basel kentinde doğmuş 27 yaşındaki Leonhard Euler, bugün Basel Problemi olarak bilinen bu sorunun çözümünü bulmayı başardı. Euler, sonsuz toplamın sonucunun şu şekilde olduğunu gösterdi.
Ancak Euler, daha genel bir soruna odaklanmaya karar verdi. Onu ilgilendiren yalnızca kare sayıların terslerinin toplamı değil, aynı zamanda küp, dördüncü ve daha yüksek kuvvetlere sahip sayıların terslerinin toplamlarıydı.
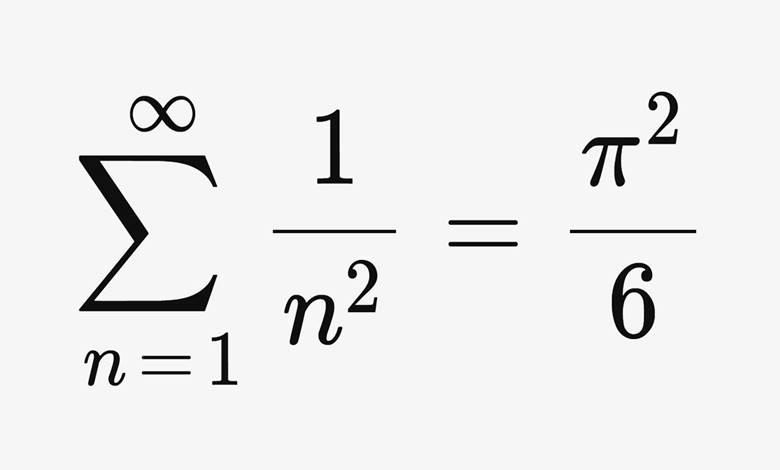
Bu problemi çözmek için, Euler bugün zeta fonksiyonu olarak bilinen ζ(s) fonksiyonunu tanımladı. Basel problemi, zeta fonksiyonlarının sadece bir özel durumu olup ζ(2) değerine karşılık gelir. Euler, zeta fonksiyonunun tüm çift tam sayı değerleri (s = 2k) için sonucu hesaplamayı başardı. Euler, ζ(2), ζ(4), ζ(6) gibi değerleri kesin formüllerle ifade etti. Ayrıca bunların π’nin kuvvetleriyle bağlantılı olduğunu keşfetti.
Ancak Euler, s tek sayı olduğunda sonucun nasıl değiştiğini açıklığa kavuşturamadı. Ayrıca, ζ(3), ζ(5), ζ(7) gibi değerlerin irrasyonel olup olmadığını ya da bir kesirle ifade edilip edilemeyeceğini belirleyemedi. Euler’in çözüm getiremediği bu problem, daha sonra Roger Apéry’nin 20. yüzyıldaki çığır açan ispatına kadar açık bir soru olarak kalmaya devam etti.
Zeta Fonksiyonu Neden Önemlidir?
Sonraki yıllarda ve on yıllarda, zeta fonksiyonu büyük ilgi gördü ve günümüzde matematiğin en büyük gizemlerinden biriyle yakından bağlantılı hale geldi. Bunun nedeni 19. yüzyılda, Alman matematikçi Bernhard Riemann’ın zeta fonksiyonunu sadece doğal sayılar için değil, aynı zamanda karmaşık sayılar için de değerlendirmesiydi.
1859 yılında, Riemann bu genişletilmiş zeta fonksiyonunu kullanarak, daha sonra Riemann Hipotezi olarak ün kazanacak olan iddiasını ortaya attı. Riemann Hipotezi’nin çözülmesi, matematik dünyasında büyük bir dönüm noktası olacaktır. Hipotezi kanıtlayan veya çürüten kişi, bir milyon dolarlık ödülü kazanma hakkına da sahip olacaktır.
Zeta fonksiyonuna gösterilen tüm ilgiye rağmen, kimse ζ(3)’ün tam değerini belirlemeyi başaramadı. Ancak, 20. yüzyılda ζ(3)’ün fizikte ortaya çıkmasıyla işler daha da ilginç hale geldi. Bu özel değer, kuantum mekaniği ve elektrodinamik gibi alanlarda beklenmedik şekillerde kendini göstermeye başladı. Bu gelişme, yalnızca sayı teorisi açısından değil, modern fiziğin temel ilkeleri açısından da ζ(3)’ün önemini artırdı.
1940’lı yıllarda, araştırmacılar elektromanyetizmanın kuantum teorisini formüle etmeyi başardılar. Bu teoriye göre, vakum aslında tam anlamıyla boş değildir. Bunun yerine, çok kısa ömürlü parçacık-karşıt parçacık çiftleri içerir. Bu parçacık çiftleri, adeta yoktan var olup hemen yok olan bir tür kuantum parıltısı oluşturur.
Elektrodinamik süreçleri, örneğin iki elektronun saçılmasını açıklamak istediğinizde, bu sürekli oluşup yok olan parçacıkları da hesaba katmanız gerekir. Çünkü bu geçici parçacık-karşıt parçacık çiftleri, elektronların hareketini saptıracaktır. İşte bu kuantum etkisini açıklamak için ζ(3) değeri kullanılmaktadır. Fiziksel hesaplamalar için, ζ(3) değerinin birkaç ondalık basamağını bilmek yeterlidir. Ancak matematikçiler, için bu asla yeterli olmayacaktır.
Apery Sabiti Nedir?
Apéry, ζ(3) fonksiyonunun irrasyonel olduğunu ispatlamayı başardı. Apéry’nin ispatı, daha önce bilinmeyen bir ζ(3) seri açılımına dayanıyordu. Fransız matematikçinin bu olağanüstü çalışmasını onurlandırmak için ζ(3)’ün değeri artık “Apery Sabiti” olarak bilinmektedir. Ancak bu, ζ(3) ile ilgili tüm soruların çözüldüğü anlamına gelmez.
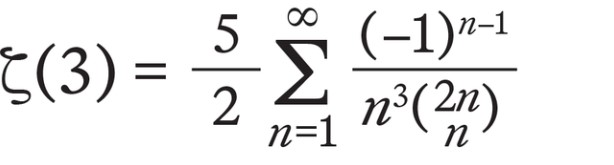
Uzmanlar hâlâ ζ(3)’ün basit matematiksel sabitlerle ifade edilecek bir kesin değere sahip olup olmadığını araştırmaktadır. Örneğin, ζ(2) = π² / 6 şeklinde açık bir formülle tanımlanır. Ancak Apery Sabiti için böyle bir formül henüz bulunamamıştır. Bugün hâlâ Apery Sabitinin tam olarak hangi matematiksel yapıyla bağlantılı olduğunu anlamaya çalışıyoruz ve bu sorunun cevabına ulaşmaktan oldukça uzağız.
Kaynaklar ve İleri Okumalar:
- Mysterious Constant that Makes Mathematicians Despair. Yayınlanma tarihi: 19 Aralık 2024. Kaynak site: Scientific American. Bağlantı: Mysterious Constant that Makes Mathematicians Despair
- Rational or Not? This Basic Math Question Took Decades to Answer.. Yayınlanma tarihi: 5 Ocak 2025. Kaynak site: Quanta Magazine. Bağlantı: Rational or Not? This Basic Math Question Took Decades to Answer.
Size Bir Mesajımız Var!
Matematiksel, matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel