1913’te Rus matematikçi Andrey Andreyeviç Markov, St. Petersburg’daki çalışma odasında, Aleksandr Puşkin’in bir romanıyla birlikte oturuyordu. Ancak Markov’un amacı kitap okumak değildi.

Bunun yerine bir kalem, kağıt aldı ve kitabın ilk 20.000 harfini, aralardaki boşlukları ve noktalama işaretlerini kaldırarak yanyana yazdı. Sonrasında da bu harfleri, her biri 10×10 karakter içeren 200 ızgaraya yerleştirdi. Ardından her satır ve sütundaki sesli harfleri saymaya başladı, sonuçları topladı.
Dışarıdan bakan birine Markov’un tüm bu yaptıkları tuhaf görünecektir. Ancak Markov kitabı yaşam ve insan doğası hakkında dersler çıkarmak için okumuyordu. Metnin matematiksel yapısını arıyordu ve aslında 1909’dan beri geliştirmekte olduğu bir olasılık teorisini test ediyordu.
19. yüzyılda Rus matematikçiler iz bırakmaya başlamıştı. Nikolai Lobachevsky (1792–1856), Öklid dışı geometrinin mucitlerinden biriydi. Birkaç on yıl sonra, Pafnuty Chebyshev (1821–1894), sayılar ve olasılık teorisine önemli katkılarda bulunmuştu.

Chebyshev’in öğrencileri, bir sonraki nesil Rus matematikçilerinin çekirdeğini oluşturdu; Markov da bunlardan biri idi. Kendisi tüm kariyerini St. Petersburg Üniversitesi’nde (Chebyshev ve diğerleriyle birlikte) tamamladı. Bağlantılı olasılıklar zincirleri hakkındaki fikirlerini de, emekli olduktan sonra geliştirmeye başladı.
Andrey Markov Neden Harfleri Saydı?
Olasılık teorisinin kökleri şans oyunlarına dayanır. Buna göre adil bir madeni para atılırsa, yazı gelme olasılığı her zaman 1/2’dir. İkinci bir para atarsak, sonucun ilk atışımız ile hiçbir ilgisi yoktur. Bu bağımsızlık ilkesi bileşik olasılıkları hesaplamayı kolaylaştırır. Adil bir parayı iki kez havaya atarsanız, her iki seferde de yazı gelme olasılığı basitçe 1/2×1/2 veya 1/4’tür.
Yağmurlu bir günün olasılığının 1/3 olduğunu varsayalım. Bu, iki gün üst üste yağmur yağma olasılığının 1/3×1/3=1/9 olduğu anlamına gelmez. Kimi durumlarda gelecekteki olayların olasılıkları sistemin mevcut durumuna bağlıdır ve olaylar birbirine bağlandıkça bir Markov zinciri oluştururlar.
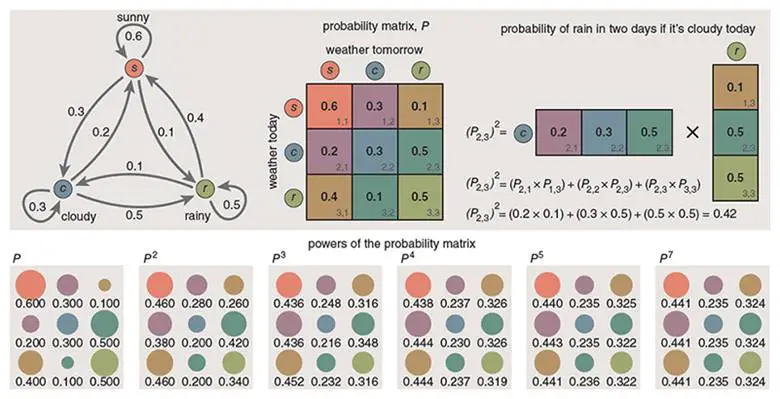
Noktalar ve oklardan oluşan bir diyagram, bir Markov zincirinin yapısını gösterir. Noktalar durumları temsil eder; oklar geçişleri belirtir. Her ok, o geçişin olasılığını veren ilişkili bir sayıya sahiptir. Bu sayılar olasılıklar olduğundan, 0 ile 1 arasında yer alır. Ayrıca bir noktadan çıkan tüm olasılıklar tam olarak toplam 1’e eşit olmalıdır. Belirli dizinin olasılığını hesaplamak için, karşılık gelen geçiş oklarıyla ilişkili olasılıkları çarpmanız yeterlidir.
Matrisin kendisi ( P diyelim) yarının hava durumunu tahmin etsin. P × P veya P 2 çarpımı yarından sonraki gün için hava durumu olasılıklarını verir. P 3 üç gün sonraki olasılıkları tanımlar, vb. Tüm gelecek bu tek matristen ortaya çıkacaktır.
Andrey Markov’un Çalışması Claude Shannon Sayesinde Hatırlandı
Andrey Markov, konu ile ilgili çalışmalarına sadece iki durumu olan bir sistem ile başlamıştı. Sonraki birkaç yıl içinde Markov bulgularını genelleştirdi ve bunun geniş bir model sınıfına uygulanabileceğini gösterdi. Bunu kanıtlamak için de bir kitaptaki harfleri saymak ona göre doğru bir yaklaşımdı.

En üstte tek bir kıta var. Altında, noktalama işaretleri ve kelime boşlukları kaldırılmış bir metin parçası gösterilir. Ünlüler ve ünsüzler beyaz ve siyah yazı tipiyle ayırt edilir. Aşağıdaki çubuk grafikler harflerin ve harf çiftlerinin sayılarını gösteriyor.
Yani Markov, ünlüleri ünsüzlerden ayırırken geliştirmekte olduğu bir olasılık teorisini test ediyordu. O noktaya kadar olasılık alanı çoğunlukla rulet veya yazı tura atma gibi önceki olayların sonucunun mevcut olayların olasılığını değiştirmediği fenomenleri analiz etmekle sınırlıydı.
Ancak Markov, çoğu şeyin nedensellik zincirleri içinde gerçekleştiğini ve önceki sonuçlara bağlı olduğunu düşünüyordu. Bu olayları olasılıksal analiz yoluyla modellemenin bir yolunu istiyordu. Bunu göstermek için, bir metinde, belirli bir harfin metinde belirli bir noktada görünme şansının, bir dereceye kadar, ondan önce gelen harfe bağlı olduğunu göstermek istiyordu.
Bu çalışmadan “An Example of Statistical Investigation of the Text Eugene Onegin Concerning the Connection of Samples in Chains, isimli bir araştırma makalesi ortaya çıkacaktı. Ancak Markov hayattayken bu çalışması fazla da dikkat çekmedi ve 2006’ya kadar İngilizceye çevrilmedi.
Bu sorun, Claude Shannon‘ın 1948’de yayınlanan İletişimin Matematiksel Teorisi (The Mathematical Theory of Communication) adlı bir makaleyle değişecekti. Shannon’ın makalesi, bir mesajdaki bilgi miktarını kesin olarak ölçmenin bir yolunu gösterdi ve bunu yaparken dijital çağı tanımlayacak bir bilgi teorisinin temellerini attı.

Claude Shannon Bir Dil Üretilebileceğini Gösterdi
Shannon, Markov’un belirli bir metinde, bir harfin veya kelimenin görünme olasılığının yaklaşık olarak hesaplanabileceği fikrinden büyülenmişti.
Sonrasında Markov gibi Shannon da metinler üzerinde deneyler yapmaya başladı. Ancak kendisi istatistiksel kurallara göre metin üretmeye çalışarak bir adım daha ileri gitti. İlk kontrol deneyinde, 27 sembolden oluşan bir alfabeden (26 harf artı bir boşluk) rastgele harfler seçerek bir cümle oluşturmaya başladı ve aşağıdaki çıktıyı elde etti:
XFOML RXKHRJFFJUJ ZLPWCFWKCYJ FFJEYVKCQSGHYD QPAAMKBZAACIBZLHJQD
İletişim kurmak için harfleri eşit olasılıkla seçmediğimizden ortaya çıkan bu cümle anlamsızdı. Ancak Andrey Markov’un gösterdiği gibi, ünsüz harfler ünlü harflerden daha olasıydı. Ayrıca E’ler S’lerden, S’ler de Q’lardan daha yaygındır. Shannon bunu hesaba katarak orijinal alfabesini İngilizcenin olasılığını daha yakından modelleyecek şekilde değiştirdi. Sonucunda İngilizceye biraz daha yakın olan bir cümle elde etti.
OCRO HLI RGWR NMIELWIS EU LL NBNESEBYA TH EEI ALHENHTTPA OOBTTVA NAH BRL.
Shannon, bir dizi sonraki deneyde, istatistiksel modeli daha da karmaşık hale getirdiğinizde giderek daha anlaşılır sonuçlar elde ettiğinizi gösterdi. Shannon, Markov aracılığıyla, İngilizce dili için bir istatistiksel çerçeve ortaya koydu. Bu çerçeveyi modelleyerek aslında dil üretebileceğini gösterdi. Son deneyde Shannon, harfler yerine bir kelime kümesinden yararlandı ve şu sonucu elde etti:
THE HEAD AND IN FRONTAL ATTACK ON AN ENGLISH WRITER THAT THE CHARACTER OF THIS POINT IS THEREFORE ANOTHER METHOD FOR THE LETTERS THAT THE TIME OF WHO EVER TOLD THE PROBLEM FOR AN UNEXPECTED.
Sonuç olarak
Hem Shannon hem de Markov’un fikirleri, daha farklı sorunları yeniden düşünmenin bir yolunu sundu. Andrey Markov olasılık teorisini bağımsız olayların ötesine taşıyarak yeni bir çağın yolunu açtı. Sonucunda Markov zincirleri günümüzde ekonomi, biyoloji, bilgisayar, pazarlama ve daha pek çok alanda kullanılır.
Örneğin, Google’ın kurucuları Larry Page ve Sergey Brin tarafından tasarlanan PageRank algoritması, durumları World Wide Web’in sayfaları olan bir Markov zincirine dayanmaktadır. Geçişler sayfalar arasındaki bağlantılardır. Algoritmanın amacı, her web sayfası için bağlantıları rastgele takip eden bir okuyucunun o sayfaya ulaşma olasılığını hesaplamaktır.
Shannon’un çalışması da bir mesajdaki bilgi birimlerini ölçmenin ve kodlamanın kesin bir yolunu formüle etmesine yardımcı oldu. Bu da telekomünikasyonda ve sonunda dijital iletişimde devrim yarattı. Tüm bu çalışmalar, dijital çağdan günümüze kadar uzanan doğal dil işleme için de yeni bir çağın habercisi oldu.
Kaynaklar ve ileri okumalar
- First Links in the Markov Chain. kaynak site: American Scientist. Bağlantı: First Links in the Markov Chain
- Andrey Markov & Claude Shannon Counted Letters to Build the First Language-Generation Models. Yayınlanma tarihi: kaynak site: Bağlantı: Andrey Markov & Claude Shannon. Counted Letters to Build the First Language-Generation Models
- Markov , A.. (2006). An Example of Statistical Investigation of the Text Eugene. Onegin Concerning the Connection of Samples in Chains. Science in Context. 19. 591 – 600. 10.1017/S0269889706001074.
Matematiksel





