Matematiğe ilgi duysanız da duymasanız da Altın Oran kavramına mutlaka bir yerde rastlamışsınızdır. Matematikte Pi (π) sayısından sonra en ünlü sayı olarak kabul edildiği bile söylenebilir.

Bu oran, popüler kültürde sıkça karşımıza çıkar. Da Vinci Şifresi kitabında ve filminde bahsedilmiş, matematiğin gerçek dünyadaki önemini vurgulamak amacıyla birçok makale, kitap ve okul projesinde kendine yer bulmuştur.
Birçok yazar, doğadaki tüm güzel desenlerin temelinde Altın Oran’ın bulunduğunu iddia eder. Hatta bazen “İlahi Oran” olarak da adlandırılır. Sanat ve mimari alanında, büyük eserlerin bu oranı temel aldığı öne sürülmüştür.
Matematikle fazla ilgilenmeyen bir kişi bile, Mısır piramitlerinin, Yunan tapınaklarının, Mona Lisa tablosunun ve hatta insan vücudunun Altın Oran’a uyduğu fikrine aşinadır. Bu iddialar, zamanla Altın Oran’a mistik bir anlam yüklenmesine neden olmuştur. Oranın doğada, sanatta ve insan vücudunda sıkça görüldüğü algısı, onu “ilahi bir güç” gibi değerlendiren görüşlerin ortaya çıkmasına yol açmıştır.

Bu matematiksel kavramın kökeni çok eskiye dayanır. Pisagor, Güney İtalya’daki Crotone şehrinde kurduğu okulda, doğanın matematiksel bir düzen içinde olduğuna inanan mistik öğretiler geliştirdi. Pisagorcular, doğanın tamamen sayılardan oluştuğunu ve her şeyin bir sayısal uyum içinde var olduğunu düşünüyorlardı. Başlangıçta bu fikirler filozoflar arasında pek ilgi görmese de, zamanla gelişerek Altın Oran anlayışına evrildi.
Altın Oran Nedir?
Bir doğru parçasını iki parçaya böldüğünüzü hayal edin. Bu parçaları A (büyük parça) ve B (küçük parça) olarak adlandıralım. Eğer bu iki parçanın toplamının büyük parçaya oranı, büyük parçanın küçük parçaya oranına eşit olursa, Altın Oran’ı elde etmiş olursunuz. Matematiksel olarak bu oran şu şekilde ifade edilmektedir.
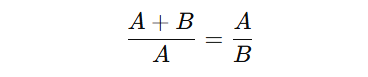
Bu denklem çözüldüğünde, Altın Oran yaklaşık 1.6180339887498… olarak bulunur ve Yunanca phi (φ) harfi ile gösterilir. Altın Oran’a “φ” harfinin verilmesinin sebebi, onu kompozisyonlarında kullanan ünlü Yunan heykeltıraş Phidias’a (MÖ 490-430) bir gönderme olmasıdır. Phidias’ın adı, Yunancada φ harfiyle başladığı için bu sembol seçilmiştir.
Altın Oran’ın değeri yaklaşık 1.618 olsa da, bu sayı 1.5’a oldukça yakındır. İnsan zihni, genellikle 1.5 civarındaki oranları Altın Oran’a benzetme eğiliminde olduğu için, onu doğada ve sanatta her yerde gördüğümüzü düşünebiliriz. Ancak bu, büyük ölçüde bir algı yanılgısıdır.

Tıpkı Pi (π) sayısı gibi, Altın Oran da irrasyonel bir sayıdır. İrrasyonel sayılar sonsuz basamağa sahip olduğundan, gerçek dünyada tam olarak uygulanamazlar. Bu yüzden, doğadaki veya sanattaki varlığı çoğu zaman yaklaşık değerler ve algılar üzerine kuruludur.
Altın Oran’a yakın bir en-boy oranına sahip olan bir dikdörtgenin, yani Altın Dikdörtgen’in, göze en hoş gelen dikdörtgen olduğu söylenir. Bunun nedeni, çok uzun ya da çok geniş olmaması ve estetik açıdan dengeli bir görünüme sahip olduğu düşüncesidir.

Ancak burada önemli bir nokta var: Bir dikdörtgenin göze hoş görünmesi için en-boy oranının tam olarak Altın Oran’a (φ ≈ 1.618) eşit olmasına gerek yoktur. Buna yakın herhangi bir oran da pekala aynı derecede göze hoş gelecektir. Aşağıdaki dikdörtgenlerden herhangi birinin göze daha güzel gözüktüğünü söyleyebilir misiniz?

Altın Oran Efsanesi Nasıl Ortaya Çıktı?
Altın oranın estetikle herhangi bir ilişkisi olduğu fikri, iki kişiden gelmektedir. Bu düşünceyi ilk ortaya atanlardan biri Luca Pacioli’dir (1445-1517). 1509 yılında “Divina Proportione” (İlahi Oran Üzerine) adlı kitabını yazmış ve bu eserde Altın Oran’ın sanattaki, mimarideki ve doğadaki öneminden bahsetmiştir.
Ancak, Pacioli’nin kitabı bilimsel özgünlüğe sahip bir çalışma olmaktan çok, dikkatli ve titiz bir derlemeydi. Altın Oran ile ilgili birçok iddiayı ortaya koymuş, ancak hiçbirini kanıtlamamıştır.
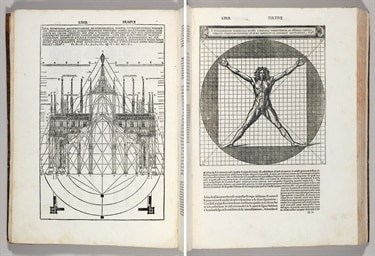
Pacioli’nin öğrencilerinden biri olan Leonardo da Vinci, dönemin saygın matematik öğretmenlerinden dersler almış, ancak kendi resimlerinde Altın Oran’ı bilinçli bir şekilde uygulamamıştır. Vitruvius Adamı adlı çalışmasını yaparken, çemberin ve karenin merkezlerinin farklı noktalarda olması gerektiğini fark etmiştir. Ancak sanılanın aksine Altın Oran’ı temel almamıştır.
Altın Oran’ın estetikle bağdaştırılması, büyük ölçüde Adolf Zeising’e (1810-1876) dayanmaktadır. Zeising, önce insan bedeninin ideal oranlarını analiz etmiş, ardından antik heykeller üzerinde incelemelerde bulunmuştur. Fakat araştırmaları bununla sınırlı kalmamış, yıldızlar, kristaller, bitkiler ve hayvanlar gibi doğadaki farklı varlıkların da Altın Oran’a uyduğunu öne sürmüştür.

1854 yılında yayımladığı “Neue Lehre von den Proportionen des menschlichen Körpers” (İnsan Bedeninin Oranları Üzerine Yeni Öğreti) adlı eserinde, Altın Oran kavramını sistematik bir şekilde ele almış ve elde ettiği bulguları paylaşmıştır.
Ona göre, Altın Oran doğanın temelinde bulunan evrensel bir yasa idi. Bu oran, sanattan mimariye, insan vücudundan evrendeki büyük yapı oluşumlarına kadar her yerde görülebilirdi.
Sanat Ve Mimaride Altın Oran Miti Nedir?
Bazı sanatçıların eserlerinde kasıtlı olarak Altın Oran’ı kullandıkları kesin bir gerçektir. Aynı şekilde, Eski Mısırlı, Romalı ve Yunan mimarların bu oranı basit geometrik aletler kullanarak ürettiklerine ve yapılarında kullandıklarına dair bazı kanıtlar bulunmaktadır.

Oran kavramı, mimarlık kuramının en temel unsurlarından biridir. Bir mimar, yalnızca bir binanın genel formunu değil, aynı zamanda kapı kollarından pencerelere kadar her öğenin diğer bileşenlerle uyum içinde olmasını sağlamak için oranlardan faydalanır.
Ancak burada göz önünde bulundurulması gereken önemli bir nokta vardır. Altın Oran, sanatta ve mimaride kullanılan tek oran değildir. Plastik Oran gibi başka matematiksel oranlar da bulunmaktadır ve birçok sanat eseri ile mimari yapı Altın Oran’a uymadığı halde estetik olarak son derece etkileyicidir.
Sonuç olarak
Fibonacci dizisi, her sayının kendisinden önceki iki sayının toplamı olduğu bir sayı dizisidir. Bu dizinin bazı elemanları, 0, 1, 1, 2, 3, 5, 8, 13, 21, 34… biçimindedir ve dizinin ardışık terimlerinin birbirine oranı altın orana giderek yaklaşır.
Fibonacci dizisi, doğada bazı yerlerde görülür. Örneğin ayçiçeklerinin tohum diziliminde, çam kozalağı sarmallarında ve bazı yaprak dizilimlerinde Fibonacci sayılarına rastlanabilir. Ancak bu, evrenin doğrudan Fibonacci dizisine göre tasarlandığı anlamına gelmez. Aslında, bitkilerin büyüme düzenleri, güneşe ve besine en iyi şekilde erişim sağlamak için evrimsel bir stratejinin sonucudur.

Bu tür matematik mitlerinin yanıltıcı bir etkisi olur. Özellikle öğrencilere yanlış bilgiler verilirse, matematiğin gerçek işleyişi hakkında yanlış bir algıya kapılmaları mümkündür. Bu yüzden öğretmenlerin ve araştırmacıların, bilimsel ve doğru bilgileri aktarmaları önemlidir.
Eğer bir sonraki proje konunuz “Altın Oran Nedir? Doğada Nerede Görülür?” olacaksa, bu konunun bilimsel gerçekler ve popüler mitler açısından ele alınması gerektiğini aklınızda bulundurun.
Kaynak ve ileri okumalar:
- Naini, F.B. The golden ratio—dispelling the myth. Maxillofac Plast Reconstr Surg 46, 2 (2024). https://doi.org/10.1186/s40902-024-00411-2
- Mark Chu-Carroll; A Geek’s Guide to the Beauty of Numbers. Logic, and Computation; 2013 The Pragmatic Programmers, LLC.
- Myths of maths: The golden ratio; yayınlanma tarihi: 23 Şubat 2020; Bağlantı: https://plus.maths.org/
- Martines, G. The Relationship Between Architecture and Mathematics in the. Pantheon. Nexus Netw J 2, 57–62 (2000). https://doi.org/10.1007/s00004-999-0008-6
- The Golden Mean: a great discovery or natural phenomenon? Yayınlanma tarihi: 3 Kasım 2013. Kaynak site: Conversation. Bağlantı: he Golden Mean: a great discovery or natural phenomenon?
Matematiksel