1952 yılında, kod kırma ve yapay zekâ konularındaki çalışmalarıyla tanınan Britanyalı matematikçi Alan Turing, yaşadığı kişisel trajediye rağmen, sıradan ve tekdüze yapılardan nasıl desenlerin ortaya çıkabileceğini açıklayan bir mekanizma önerdi. Günümüzde bilim insanları hâlâ bu modeli kullanıyor ve yeni yorumlarla zenginleştirerek hayvanlardaki desenleri daha iyi anlamaya çalışıyor..

.
Moda tasarımcılarının hayvan desenlerinden ilham almasının bir nedeni var. Doğada canlılar, baş döndürücü çeşitlilikte desenler geliştirmiştir. Bazı desenler basit ya da rastlantısal şekilde oluşur. Ancak bazıları, desen üreten sistemlerin karmaşık ve hassas etkileşimleriyle meydana gelir.
Kediler ve köpekler gibi memelilerin beyaz karınlara sahip olması oldukça basit bir mekanizmaya dayanır. Embriyo gelişirken, pigment üreten hücreler gelecekte omurga olacak hat boyunca oluşur ve oradan aşağıya, karın bölgesine doğru göç eder. Ancak bu hücreler her zaman hedeflerine tam olarak ulaşamaz. Pigment hücreleri yolun sonuna kadar varamadığında, o noktada beyaz alanlar oluşur.

Dalmaçyalı köpeklerin üzerindeki siyah benekler rastgele oluşur. Aynı şekilde, tekir (calico) kedilerdeki siyah ve turuncu lekeler de rastlantısaldır. Ancak sincapların ve kaplanların çizgileri, balıklar ve tavuklardaki benekler gibi birçok hayvanın göz alıcı desenleri son derece hassas bir şekilde oluşur. Bu olağanüstü öz-organizasyon sürecinde, başlangıçta tekdüze olan bir yüzey düzenli bir desene dönüşür.
Bu sürecin nasıl işlediğini çözen kişi Alan Turing’di. Onu, yapay zekânın temelini atan 20. yüzyılın önemli matematikçilerinden biri olarak tanıyor olabilirsiniz. Ancak Turing, matematik bilgisini gelişmekte olan embriyoda düzenli yapıların nasıl ortaya çıktığını anlamak için de kullandı.
O günden bu yana bilim insanları, Turing denklemlerini parmak izi çizgilerinin oluşumu, tüylerin çıkacağı yerlerin belirlenmesi ve çizgi ya da benek gibi renk desenlerinin gelişimi gibi birçok alana uyguladı. Ve görünen o ki Turing gerçekten doğru bir iz üzerindeydi. Bugün hayvan desenlerini inceleyen bilim insanları, özellikle başka etkenlerle birleştirildiğinde, Turing’in fikirlerinin hâlâ son derece geçerli olduğunu söylüyor.
Turing Denklemleri Nedir?
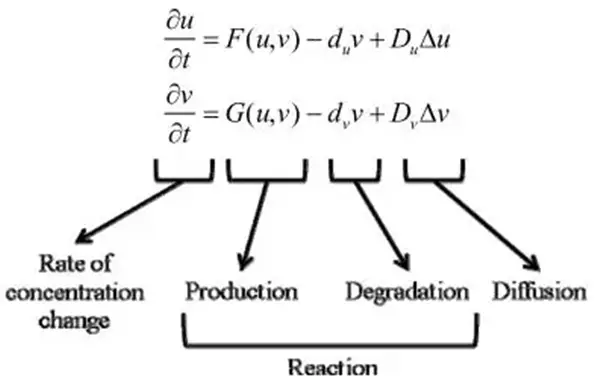
Benek oluşturan sistem, Turing desenlerinin en temel versiyonudur. Turing’in “morfojen” adını verdiği bu modelde, gelişmekte olan deri boyunca hareket edebilen iki ana madde yer alır. Bunlardan biri etkinleştirici, diğeri ise baskılayıcıdır. Etkinleştirici hem kendini hem de baskılayıcıyı aktive eder. Baskılayıcı ise etkinleştiricinin etkisini engeller.
Tek başına bu sistem fazla bir etki yaratmaz. Ancak bu maddeler dokularda farklı hızlarla yayılırsa ve sisteme rastgele dalgalanmalar eklenirse, kürk, tüy ya da pullar üzerinde kalıcı benek desenleri oluşabilir.

Diyelim ki etkinleştirici bazı bölgelerde rastgele etkinleşiyor. Kaynağından yayılırken hem kendisini hem de baskılayıcıyı devreye sokar. Eğer baskılayıcı, etkinleştiriciden daha hızlı yayılırsa, lokal olarak etkinleştiriciyi tamamen bastıracak kadar yoğunlaşamaz. Sonuçta, çevresi baskılayıcıyla çevrili, dengeli ve eşit aralıklı etkinleştirici benekleri ortaya çıkar.
Sistemin parametreleri, morfojenlerin yayılma hızı, hareket ettikleri alanın büyüklüğü ya da şekli gibi faktörler, deseni değiştirebilir. Örneğin çitanın kuyruğu uzun ve incedir. Bu dar alanda benekler birleşir ve çizgilere dönüşür. Ancak basit bir mekanizma, şaşırtıcı derecede çeşitli ve zengin desenler yaratabilir.
Ancak doğadaki muazzam desenleri açıklamak için bazen Turing denklemleri tek başına yeterli olmaz. Bilim insanları bu durumda ek unsurları devreye sokmak zorunda kalır. Basitçe yayılan kimyasallar yerine, doğrudan hücrelerin kendisi desen oluşumuna katılabilir. Ya da morfojenlerin dokular arasında taşınması veya desenlerin daha keskin ve belirgin hale gelmesi için hayvanlar ek stratejiler geliştirmiş olabilir.

Bilim insanları, Turing desenlerinin başka desen oluşturma mekanizmalarıyla iç içe geçtiği ya da ikiden fazla morfojenin etkileşimde bulunduğu son derece karmaşık örneklerle de karşılaşıyor. Bu durumlar, desen oluşumunun yalnızca bir modelle değil, çok katmanlı biyolojik süreçlerin bir bileşimiyle gerçekleştiğini gösteriyor.
Günümüzde Hayvanların Vücutlarındaki Desenleri Daha İyi Anlıyoruz

Gelişim biyologlarının en çok başvurduğu model canlılardan biri olan zebra balıkları başından kuyruk yüzgecine kadar uzanan net siyah ve sarı çizgilere sahiptir. Bu durumda, deseni oluşturan şey yayılan kimyasallar değil, pigment hücreleri arasındaki daha karmaşık etkileşimlerdir.
Hücreler iki ana tiptir: siyah melanoforlar ve sarı ksantoforlar. Yakın mesafede bu hücreler birbirini iter ya da yok eder. Aralarındaki bu rekabet, onları balık vücudu boyunca belirgin çizgiler halinde ayırır. Ancak aynı zamanda siyah hücreler, sarı hücrelerden —henüz tanımlanamamış— bir madde almazlarsa ölürler. Bu nedenle melanoforlar, kendilerini korumak için ksantoforlara belli bir mesafede kalırlar.
Turing denklemlerine göre, siyah hücrelerin sarı hücrelerden ihtiyaç duyduğu madde difüzyon yoluyla ulaşmalıydı. Ancak araştırmacılar sarı hücrelerden gelen bu maddenin, siyah hücrelere ulaşmak için moleküler ölçekte oldukça uzun bir mesafeyi kat etmek zorunda olduğunu keşfettiler.. Bu durumda da difüzyon verimli çalışmaz.
Zebra balığının desen oluşturma süreci incelenirken, “leopar” adı verilen bir mutant varyant dikkat çekti. Bu mutant, normalde zebra balıklarında gördüğümüz çizgili desenlere sahip değil. Onun yerine vücudu beneklerle kaplı.

Bilim insanları bu mutantın genetik yapısını incelediklerinde, bozulmuş bir gene rastladı. Bu gen, hücreler arasında bağlantı kanallarını oluşturmaktan sorumlu. Bu keşif, çizgi ve benek desenlerinin nasıl oluştuğuna dair Turing mekanizmasına biyolojik bir katman daha ekliyor. Desen sadece kimyasalların yayılmasıyla değil, hücreler arası aktif iletişimle şekilleniyor.
Sonuç Olarak
Turing’in fikirleri, aradan on yıllar geçmesine rağmen etkisini sürdürüyor. Ancak kesin olan bir şey var. Doğa, sandığımızdan çok daha karmaşık.
Kaynaklar ve İleri Okumalar:
- Cass, J.F., Bloomfield-Gadêlha, H. The reaction-diffusion basis of animated patterns in eukaryotic flagella. Nat Commun 14, 5638 (2023). https://doi.org/10.1038/s41467-023-40338-2
- Van Gorder, Robert. (2021). A theory of pattern formation for reaction–diffusion systems on temporal networks. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences. 477. 10.1098/rspa.2020.0753.
- The mathematical theory that connects swimming sperm, zebra stripes, and sunflower seeds. Yayınlanma tarihi: 27 Eylül 2023. Bağlantı: The mathematical theory that connects swimming sperm, zebra stripes, and sunflower seeds
Size Bir Mesajımız Var!
Matematiksel, matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel





