2018 yazında, topoloji üzerine düzenlenen bir konferansta Lisa Piccirillo küçük ama ilgi çekici bir matematik problemi duydu. Bu, Teksas Üniversitesi’nde doktora öğrencisiyken geliştirdiği teknikleri sınamak için iyi bir fırsat gibi görünüyordu. Soru, ünlü matematikçi John Horton Conway’in yarım yüzyıldan uzun süre önce keşfettiği “Conway düğümünün” daha yüksek boyutlu bir düğümün kesiti olup olmadığını soruyordu.

Düğüm teorisinde bu, temel sorulardan biridir. Matematikçiler 12 veya daha az kesişimli tüm düğümler için bu sorunun cevabını bulmuştu. Ancak 11 kesişimli Conway düğümü, on yıllardır çözülmemiş bir bilmeceydi.
Piccirillo bir hafta içinde cevabı buldu. Bu çalışma ve önceki araştırmaları sayesinde, doktorasını tamamladıktan sadece 14 ay sonra, Massachusetts Institute of Technology’den kadrolu öğretim üyesi teklifi aldı.

Dördüncü boyutta düğümler nasıl olur?
Çoğumuz düğümü, iki ucu açık bir ipin birbirine dolanmış hali olarak biliriz. Oysa matematikçiler için düğüm farklı bir şeydir. Onlar ipin uçlarını birleştirir, böylece düğümün çözülmesi imkânsız hale gelir. Bu tür kapalı halkalar, son yüzyılda kuantum fiziğinden DNA’nın yapısına ve üç boyutlu uzayın geometrisine kadar pek çok alanda derin bilgiler sunmuştur.
Ancak evren yalnızca üç boyutlu değildir. Zamanı da bir boyut olarak düşünürsek, aslında dört boyutlu bir dünyada yaşarız. Bu da doğal bir soruyu gündeme getirir: Dördüncü boyutta düğümler nasıl olur?

Üç boyuttaki bir düğümü alıp dördüncü boyuta taşımak, onu çözmek için yeni bir özgürlük kazandırır. Çünkü dördüncü boyutta, iplikler birbirinin üzerinden geçer ve böylece düğüm kolayca açılır.
Eğer bir düğüm dördüncü boyutta “pürüzsüz bir yüzey” üzerinde açılırsa, o düğüme slice (dilimlenebilir) denir. Başka bir deyişle, slice bir düğüm, dört boyutta “yumuşakça çözülebilen” bir düğümdür.
1980’lerde Michael Freedman ve Simon Donaldson, dört boyutlu uzayın yalnızca pürüzsüz kürelerden oluşmadığını; aynı zamanda karmaşık biçimde buruşuk, düzleştirilemeyen küreler de içerdiğini keşfetti. Bu bulgu, bir düğümün dördüncü boyutta çözülüp çözülemeyeceğinin, hangi tür yüzeyle — pürüzsüz mü yoksa buruşuk mu — tanımlandığına bağlı olduğunu ortaya koydu.
Matematikçiler yıllar boyunca birçok düğümün topolojik olarak dilimlenebilir (yani buruşuk yüzeylerde çözülebilir) ancak pürüzsüz biçimde dilimlenemez olduğunu gösterdi. Yine de 12 veya daha az geçişe sahip düğümler arasında bir tanesi gizemini korudu: Conway düğümü.
Conway Düğümü Nedir?

John Conway, COVID-19 nedeniyle hayatını kaybetmişti. Kendisi matematiğin hemen her alanına damga vuran katkılarıyla tanınan bir bilim insanıydı. 1950’lerde düğümlerle ilgilenmeye başlamış ve 11 geçişe kadar olan tüm düğümleri listeleyen bir yöntem geliştirmişti. Ancak bu listede bir düğüm diğerlerinden farklıydı. Bu düğüm, daha sonra “Conway düğümü” olarak anılacaktı.
1980’lerdeki önemli keşiflerle birlikte matematikçiler, bu düğümün dört boyutlu uzayda düzgün bir yüzey üzerinde temsil edilebildiğini buldu. Ancak bunun pürüzsüz bir yüzeyde mümkün olup olmadığı anlaşılamadı. Düğümün yapısı o kadar karmaşıktı ki, o dönemdeki hiçbir yöntem kesin bir sonuç vermedi.
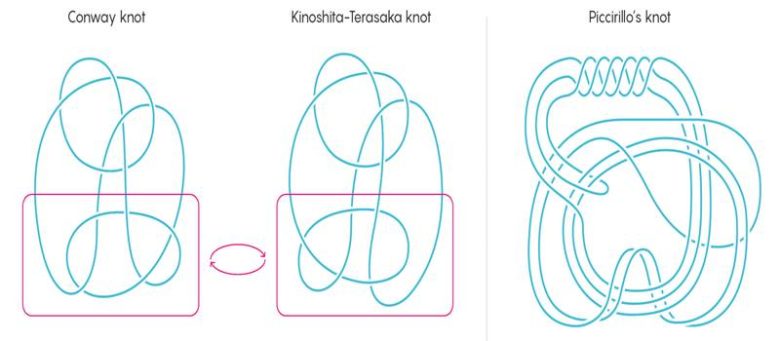
Bu zorluğun nedeni, Conway düğümünün bir “ikizinin” bulunmasıydı. Düğümü bir kâğıda çizip belirli bir kısmını kesip ters çevirir, sonra yeniden birleştirirseniz Kinoshita–Terasaka düğümü ortaya çıkar. İki düğüm o kadar benzerdi ki, aralarındaki farkı göstermek neredeyse imkânsızdı. Bu benzerlik, Conway düğümünü matematiksel testlerin çoğuna karşı görünmez kıldı.
Conway Düğümünün Çözümü Nedir?
Her düğümün, “iz” (trace) adı verilen bir dört boyutlu biçimi vardır. Bu biçim, düğümün bir dört boyutlu kürenin sınırına yerleştirilip üzerine bir kapak eklenmesiyle oluşur. Farklı düğümler aynı dört boyutlu iz yapısına sahip olabilir. Matematikçiler uzun zamandır bu “iz kardeşlerinin” ortak bir özelliği paylaştığını biliyordu.
Ancak Lisa Piccirillo ve şu anda Rice Üniversitesi’nde çalışan Allison Miller, bu iz kardeşlerinin her zaman aynı ölçüm değerlerine, yani aynı “invariant”lara sahip olmadığını gösterdi. Başka bir deyişle, iki düğüm aynı iz yapısını paylaşsa bile, sliceness açısından farklı tepkiler verebiliyordu.
Piccirillo bu düşünceyle işe başladı. Bir dizi düzenlemeyle, Conway düğümüyle aynı izi paylaşan karmaşık bir düğüm kurdu. Bu sayede, sonucun pürüzsüz biçimde dilimlenemez olduğunu buldu. Bu da doğrudan Conway düğümünün de pürüzsüz biçimde dilimlenemeyeceği anlamına geliyordu.
Sonuç Olarak
Lisa Piccirillo’nun çalışması, onlarca yıldır çözülemeyen Conway düğümüne son noktayı koydu. Basit ama zekice bir fikirle, düğüm teorisinin en inatçı problemlerinden birini çözdü. Bu sonuç, düğüm teorisinin dört boyutlu uzayın doğasını anlamada ne kadar güçlü bir araç olduğunu bir kez daha gösterdi.
Kaynaklar ve İleri Okumalar:
- Graduate Student Solves Decades-Old Conway Knot Problem; Yayınlanma tarihi: 19 Mayıs 2020. Kaynak site: Quantamagazine. Bağlantı: Graduate Student Solves Decades-Old Conway Knot Problem/
- Piccirillo, Lisa. (2018). The Conway knot is not slice. 10.48550/arXiv.1808.02923.
Size Bir Mesajımız Var!
Matematiksel, matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel





