2024 Yılına Damga Vuran 6 Matematiksel Keşif!

2024 yılı, matematik açısından parlak bir yıl oldu. Matematikçiler şimdiye kadarki en büyük asal sayının keşfinden tutun da Bach’ın müziğindeki gizemli desenlere kadar birçok keşfe imza attılar. Bu keşiflerden bazıları pratikte oldukça faydalı. Diğerleri ise pratikte henüz faydasız görünseler de son derece büyüleyici. İşte 2024 yılına damgasını vuran o keşifler!

1) Yeni Keşfedilen Bir Şekil: Yumuşak Hücreler

Öyle bir şeklimiz olsun ki bu şekil, hem en az köşeye sahip olsun hem de boşluksuz bir yüzeyi onunla tamamen kaplayabilelim. Mesela boşluksuz bir yüzeyi dairelerle kaplamaya çalıştığımızı düşünelim. Yüzeyi tamamen kaplamamız mümkün değildir, çünkü daireler birbirleriyle tam olarak örtüşmezler ve arada boşluklar kalır.

Bu basit soru mozaikleme olarak da adlandırılan, bir yüzeyi boşluk ya da üst üste binme olmaksızın dolduran karo ya da hücre denen şekillerin düzenlenmesi olan tesselasyon geometrisiyle ilgilidir. Aslında tesselasyon geometrisinin kökeni Sümerler’e kadar uzanıyor. Ancak matematikçi Gábor Domokos ve ekibine kadar kimse hücrelerin ne kadar az köşeye sahip olabileceğini düşünmemişti.

Tesselasyon geometrisi, sanattan mimariye kadar birçok alanda karşımıza çıkmaktadır.

Domokos ve ekibi bu soruyu araştırmaya başladıklarında hücre başına ortalama köşe sayısını ikinin altına düşüremeyeceklerini gördü. Araştırmalarına devam ettiklerindeyse konunun daha önce hiç araştırılmadığını fark ettiler. Bunun üzerine aşina olduğumuz geometrik şekilleri 2 köşeli forma dönüştüren bir algoritma kullanarak şekiller ürettiler.

2 boyutlu yumuşak hücre örnekleri (birinci sütun) ve doğada nerede karşımıza çıktıkları (ikinci-üçüncü sütun). Dördüncü sütunsa Zaha Hadid’in mimari çizimlerinde yumuşak hücrelerden faydalandığı örnekleri gösteriyor. (Kaynak: Domokos et al., *PNAS Nexus* 2024)

Ekip 2 boyutlu yumuşak hücreleri (soft cell) inceledikten sonra 3 boyutlu yumuşak hücreler üzerine çalışmaya başladı. Bunun üzerine 3 boyutlu yumuşak hücrelerin köşesiz de olabileceğini gördüler.

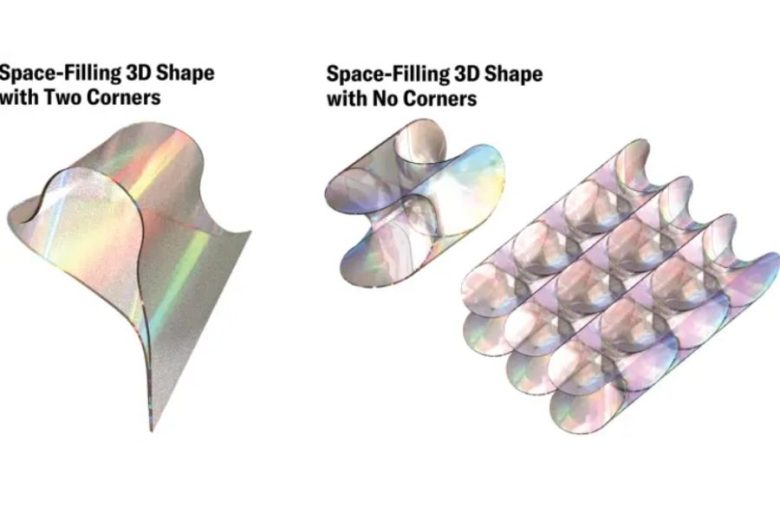
Solda 3 boyutlu 2 köşeli bir yumuşak hücre, sağda ise hiç köşesi olmayan 3 boyutlu bir yumuşak hücre. (Kaynak: “Soft Cells and the Geometry of Seashells,” Domokos et al. ; arXiv:2402.04190)

Tıpkı 2 boyutlu yumuşak hücreler gibi 3 boyutlu yumuşak hücreleri de doğada görebiliyoruz. Örneğin notilus kabuğunun kıvrımlarını oluşturan şekil, 3 boyutlu yumuşak hücrelere güzel bir örnektir.

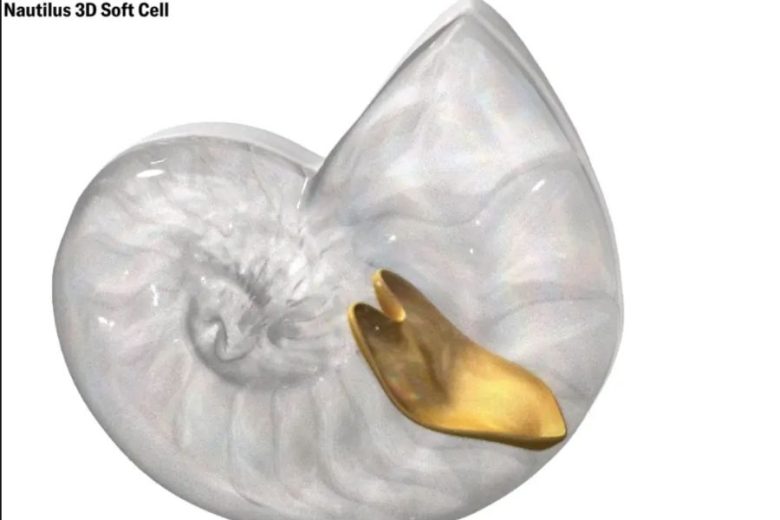
Bir deniz canlısı olan notilusun kabuğunda yumuşak hücreleri görebiliriz. (Kaynak: “Soft Cells and the Geometry of Seashells,” Domokos et al. ; arXiv:2402.04190)

Yeni keşfedilen bu şekiller doğada birçok yerde karşımıza çıkmasına rağmen yumuşak hücrelerin matematiği ve biyoloji arasındaki bağlantı şimdilik bir gözlemden ibaret. Fakat matematikçiler ve biyologlar bundan birkaç yıl sonra söz konusu bağlantının kurulacağını umut ediyor.

2) Bilinen En Büyük Asal Sayı Artık 41 Milyon Basamaklı!

Amatör matematikçi Luke Durant, 6 yıl aradan sonra bilinen en büyük asal sayının güncellenmesini sağladı. Yeni asal sayı akıllara durgunluk verecek kadar büyük. Tam olarak 41 milyon 24 bin 320 basamaklı! Bu basamak sayını daha iyi anlamlandırabilmek için şunu düşünebiliriz. Bugünkü bilgilerimize göre gözlemlenebilir evrendeki tahmini atom sayısı 10⁸⁰ . Yani 1’in yanında 80 tane 0 olan bir sayı.

En büyük asal sayı diye bir şey yoktur. Çünkü biliyoruz ki asal sayılar sonsuz tanedir. Ancak şu an için bilinen en büyük asal sayı bu biçimdedir.

Elbette bu denli büyük bir asal sayı kulağa ilk başta faydasız gelecektir. Ancak unutmayın, veri güvenliğimizin temelinde asal sayılar yatıyor. Ve daha büyük asal sayılar bir bakıma aşılması daha zor güvenlik önlemleri demek. (Konu hakkındaki daha detaylı yazımız için: Bilinen En Büyük Asal Sayı Artık 41 Milyon Basamaklı!)

3) Fizikçiler Pi Sayısı İçin Tesadüfen Yeni Bir Formül Keşfetti

Bir çemberin çevresinin çapına oranına karşılık gelen π sayısı, 4000 yıldır hayatımızda olan bir sayı. Buna rağmen bu irrasyonel sayının değerini hesaplamak her zaman zor olmuştur. Bir fizik araştırması ise π sayısını hesaplamanın yeni bir formülünü ortaya koyuyor.

Hindistan Bilim Enstitüsü’nde fizikçi olan Arnab Priya Saha ve Aninda Sinha, sicim teorisi üzerine çalışırken π’yi hesaplamanın yeni bir yolunu buldular. Saha ve Sinha aslında π için yeni bir formül bulmayı amaçlamamıştı. Ancak sicimlerin birbirleriyle nasıl etkileşime girebileceğini araştırırlarken π ile ilgili yeni bir formül keşfettiler.

Pi sayısı için tesadüfen yeni bir formül keşfeden fizikçi Aninda Sinha (solda) ve Arnab Saha.

Aslında Sinha ve Saha’nın keşfettiği formül 15. yüzyılda yaşamış Hintli bilgin Madhava’nın formülünü andırıyor. Madhava, π’nin 1 ile başlayıp 1/3, 1/5, 1/7 şeklinde devam eden toplamın sonucunun 4 katına eşit olduğunu bulmuştu.

Hintli bilgin Madhava’nın π için ortaya koyduğu formül.

Saha ve Sinha ise Madhava’nın formülünün aslında genel bir denklemin özel hali olduğunu fark etti. Çalışmaları sırasında keşfettikleri formül ise şöyleydi:

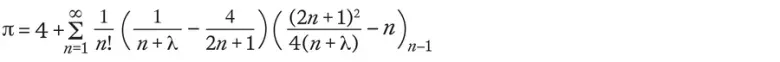
Görüldüğü üzere bu formül sonsuz bir toplam üretir. İlginç olan ise, toplamın λ gibi keyfimize göre seçtiğimiz bir parametreye bağlı olmasıdır. Yani λ değeri ne olursa olsun sonuç her zaman π’ye eşit olacaktır.

Bu noktada λ sonsuz büyükse denklem Madhava’nın formülüne karşılık gelmektedir. Çünkü λ sadece paydada olduğu için λ = ∞ olduğunda sonuç sıfır olur. Dolayısıyla λ = ∞ için denklem şu hali alır:

Bu formüle baktığımızda ilk kısım Madhava’nın formülüne benzer. Fakat (-n)_n-1 kısmı yabancı gelmiş olabilir. (-n)’in alt indisi olan n-1, Pochammer sembolü olarak adlandırılır. Genel olarak (a)_n ifadesi a x(a+1)x(a+2)x…x(a+n – 1) çarpımına karşılık gelir. Örneğin (5)₃ =5.6.7=210 gibi. Dolayısıyla Sinha ve Saha’nın keşfettiği yeni formülün 600 sene önce keşfedilen formülü de içerdiğini söyleyebiliriz.

4) Matematikçiler Tekerleği Yeniden İcat Etti

1980’lerde matematikçi Oded Schramm şöyle bir soru ortaya attı. Herhangi bir boyutta minimum hacme sahip sabit genişlikli şekilleri nasıl bulabiliriz? Soru oldukça ilginç bir soru ancak tekerleğin yeniden icadı tam da bu sorunun bir sonucu.

Schramm’ın bu sorusuyla ilgilenen araştırmacılar, yeni bir tür çok boyutlu tekerlek tasarladılar. Bu yeni tekerlek, daire ya da küre gibi geleneksel yuvarlanan şekillerden küçük boyutlarda, hatta her boyutta inşa edilebiliyor. Peki ama nasıl?

Tekerlek yuvarlanır çünkü sabit genişliğe sahip bir nesnedir. Örneğin pinpon topunu iki elimizin arasında hareket ettirdiğimizde paralel ellerimizin birbirine yaklaşmadığını veya uzaklaşmadığını görürüz. Çünkü pinpon topu sabit genişlikte bir nesnedir. Yumurta gibi sabit genişlikte olmayan bir nesnede aynı durumu gözlemlemeyiz.

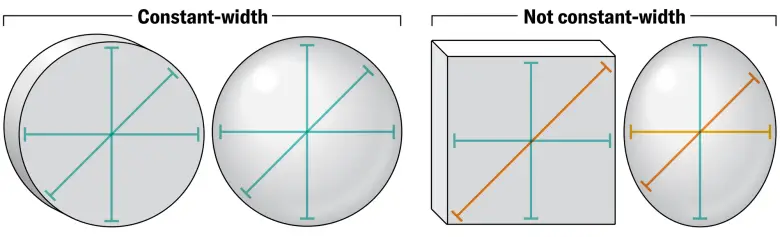
Solda sabit genişliğe sahip nesneler, sağda ise sabit genişliğe sahip olmayan nesneler gösterilmektedir.

2024 yılında yapılan çalışmaysa Reuleaux kesişim yönteminden yararlanarak herhangi bir boyutta sabit genişlikli nesneler oluşturmak için genel bir algoritma sunuyor. Ve bu algoritma en basit şekliyle şöyle çalışıyor:

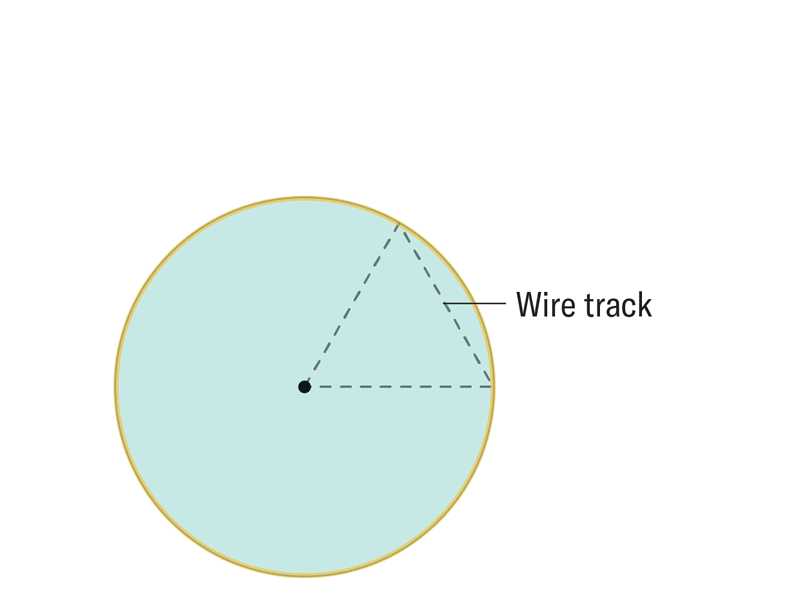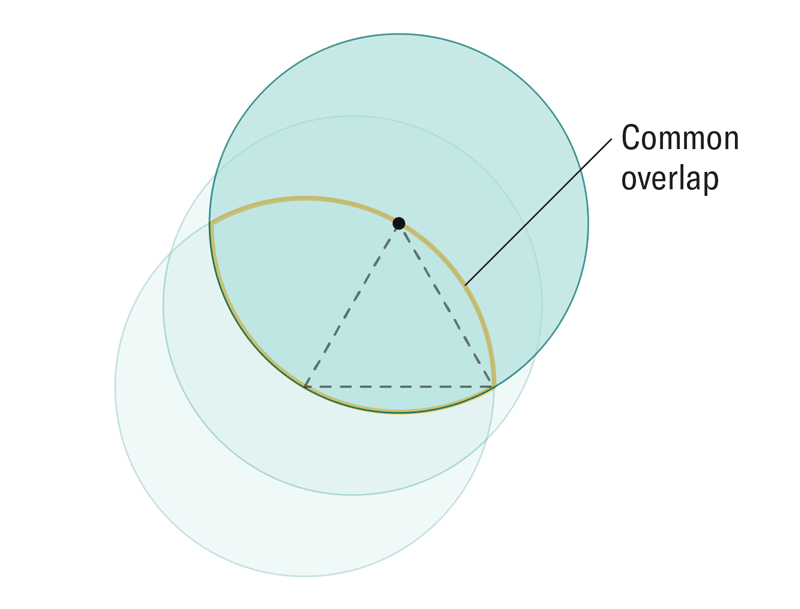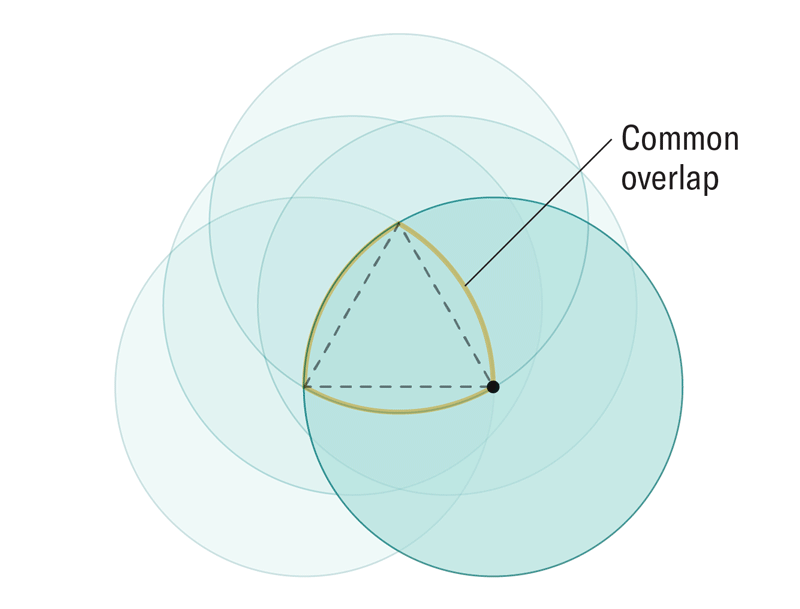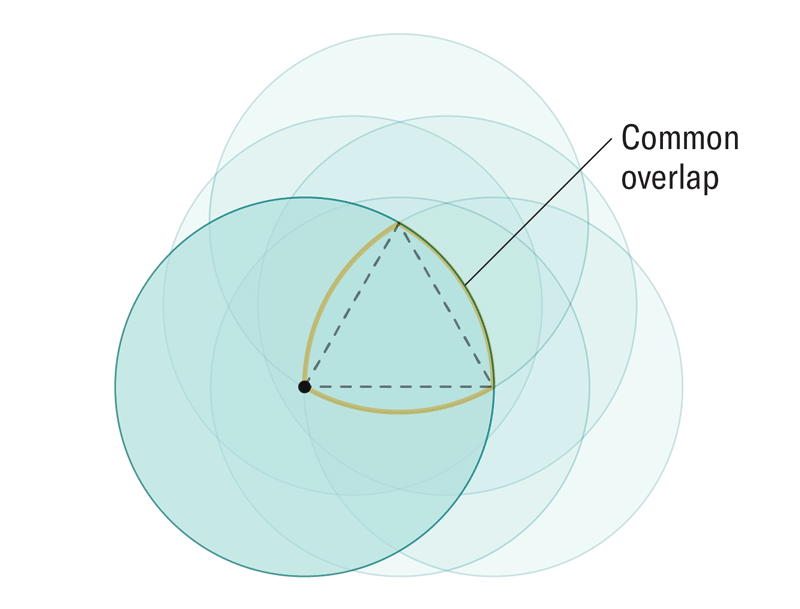
İki boyutlu sabit genişliğe sahip bir şekil elde etmek için önce eşkenar üçgen çiziyoruz. Ardından bu üçgenin etrafında merkezlenen ve üçgenin kenar uzunluğu kadar yarıçapa sahip bir daire çiziyoruz. Sonra bu daireyi merkezi üçgenin kenarlarını takip edecek şekilde hareket ettiriyoruz. Daire hareket ettikçe oluşan kesişimler bize iki boyutlu sabit genişlikli şeklimizi vermektedir. (Kaynak: Scientific American)

Algoritmayı takip ettiğimizde oluşan şekil, Reuleaux üçgenin bir genellemesi olan Reuleaux tekerleğidir. Bu sayede dairemizi etrafında sürüklediğimiz sınır, her boyut için doğru seçildiği sürece herhangi bir boyutta sabit genişlikte bir nesne üretebiliyoruz. (Konu hakkındaki daha detaylı yazımız için: Matematikçiler Onlarca Yıllık Geometri Problemini Çözmek İçin Tekerleği Daha Yüksek Boyutlarda Yeniden İcat Ediyor)

5) Meşgul Kunduz Problemi

Macar matematikçi Tibor Radó, 1962 yılında meşgul kunduz problemi adında bir problem ortaya attı. Bu problem, basitçe durma noktasına gelen n durumlu bir Turing makinesinin durmadan önce gerçekleştirebileceği maksimum adım sayısı hakkındaydı.

Bu soruyu genel olarak yanıtlamak için durma problemini çözmemiz gerekir. Yani hangi Turing makinesinin durduğunu ve hangilerinin durmadığını bilmemiz gerekir. Ancak Alan Turing, bunu bilmenin imkansız olduğunu göstermiştir. Bu da BB(n) şeklinde ifade edilen meşgul kunduz (busy beaver) fonksiyonunun tüm olası durum sayıları için hesaplanamayacağı anlamına gelir.

Alan Turing’in 1936 tarihli makalesinde sözünü ettiği makine günümüzde Turing makinesi olarak bilinmektedir. Görselde bir Turing makinesi görüyorsunuz.

Fakat Macar matematikçi Radó, meşgul kunduz fonksiyonunun ilk 3 değerini hesaplamayı başarmıştır. BB(1)=1, BB(2)=6 ve BB(3)=21. Fonksiyondaki n değeri (durum sayısı) arttıkça hangi Turing makinesinin duracağını bilmek zorlaştığından matematikçiler fonksiyonun hesaplanamaz olduğunu düşünüyordu. Nitekim son büyük meşgul kunduz problemi başarısı da 1983 yılında Allen Brady’nin BB(4)’ün 107’ye eşit olduğunu kanıtlamasıyla gerçekleşmişti.

40 yılı aşkın bir süredir ise birçok matematikçi BB(5)’in hesaplanabilirlik sınırının ötesinde olabileceğini düşünüyordu. Fakat Busy Beaver Challenge adlı uluslararası bir işbirliği projesi BB(5) değerini bulmayı başardı. Buna göre BB(5) değeri 47 milyon 176 bin 870’e eşit. Yani 5 durumlu bir program durmadan önce maksimum 47,176,870 adım atabilir veya hiç durmaz.

6) Bach’ın Müziğindeki Gizli Matematik

Alman besteci Johann Sebastian Bach, o kadar titiz bir şekilde müzik üretmiştir ki, eserleri sıklıkla matematikle ilişkilendirilir. Nitekim bu sene yapılan bir çalışmada araştırmacılar, Bach’ın notalarını matematiksel ağlara dönüştürdü. Böylece farklı stillerin nasıl değiştiğini analiz ettiler. Ve Bach’ın müziğinin matematiksel ve duygusal bilgiler de dahil olmak üzere çeşitli mesajları nasıl ilettiğini açıklamak için bilgi teorisini kullandılar.

Notaları düğüm ve kenar adı verilen çizgilerle basit nokta ağları olarak temsil eden araştırmacılar, Bach’ın yüzlerce bestesindeki bilgiyi ölçtüler. Buna göre, Bach’ın farklı müzik tarzlarının ilettikleri bilgi miktarı bakımından farklılık gösterdiği ortaya çıktı. Ayrıca araştırmacılar, Bach’ın eserlerindeki müzikal ağların dinleyicilerin mesajlarını anlamalarını kolaylaştırabilecek yapılar içerdiğini ortaya koydu. (Konu hakkındaki daha detaylı yazımız için: Bach’ın Müziğinin Aktardığı Bilgiyi Ölçmek Mümkün mü? Matematikçiler Evet Diyor!)

Kaynaklar ve İleri Okumalar