Bir kesir verildiğinde çoğu zaman onu sadeleştirmek gerekir. Ancak kesir, büyük sayılardan oluşursa, bu çok da kolay bir işlem değildir. İşte bu gibi bir durumda farkında olmadan bir çoğumuz Öklid algoritmasının bir biçimini kullanırız.
Diyelim ki kesrimiz 4356207 / 1728941 ve biz de bu kesri sadeleştirmek istiyoruz. Bunun için 1728941 ve 4356207 sayılarının en büyük ortak bölenini bulmamız gereklidir. Ancak, tahmin edeceğiniz gibi bunu yapmak çok da kolay değildir.
Öklid algoritması, a ve b sayılarının en büyük ortak bölenini bulmanın bir yoludur. Basitçe açıklamak gerekirse Öklid algoritmasını kullanırken verilen iki sayıyı sürekli olarak birbirinden çıkartıyoruz. Sonrasında fark ile çıkartılan sayı için aynı şeyi tekrarlıyoruz. Bu işleme fark sıfır olana kadar devam ediyoruz. Fark sıfır olduğunda anda çıkarttığımız son sayı bizim en büyük ortak bölenimiz oluyor.
İnsanlar Öklid adını duyduklarında genelde geometriyi düşünürler. Ancak bu yanlıştır. Kendisinin sayılar teorisine de önemli katkıları vardır. Bu algoritma ise Elementler isimli kitabın 7. cildinde, 2. önerme olarak tanımlanmıştır.

Öklid Algoritması Nedir?
Örneğin 18/24 kesrini sadeleştirmek isteyelim. Bu durumda bu ikilinin en büyük ortak bölenini ( EBOB) almamız gerekir. a = 24 ve b = 18 biçiminde düşünürsek a ve b’nin en büyük ortak böleninin aynı zamanda a – b’nin de bir bölenidir.
O zaman bu iki sayıyı birbirinden çıkartalım. Şimdi elimizde farkımız 6 var. Çıkartılan sayımızda 18. Yapmamız gereken şimdi de bu iki sayıyı birbirinden çıkartmak. Yani 18-6= 12. Bu mantığa devem edersek elde edeceğimiz sonuç EBOB(24, 18) = EBOB(18, 6) = EBOB(12, 6) = EBOB(6, 6) = EBOB(6, 0)= 6 olacaktır.
Ancak örnek olarak küçük sayıları seçmemizin nedeni, aslında algoritmayı bu biçimde kullanmanın pek de pratik olmamasıdır. Yani sayılar büyüdükçe Öklid’in yaptığı gibi sadece çıkarma kullanmak pek doğru olmaz. Örneğin, EBOB (101, 10100 + 1) için sonucu tekrar tekrar çıkarma ile bulmaya çalışırsak bu işlemi 1098 kez tekrarlamamız gerekir. Bu da elbette hızlı bir yöntem değil.
Bu nedenle işin içine çıkarmanın kısa yolu olan bölme işlemini sokmamız gerekir. Yani Öklid algoritmasını kullanırken sayıları defalarca birbirinden çıkartacağımıza iki sayıyı birbirine bölüp, kalanı elde ederek de algoritmayı uygulamaya devam edebiliriz.
Öklid Algoritması İle İlgili Bir Örnek
1015 ve 231’in EBOB’unu bu şekilde bulalım. Önce 1015’i 231’e bölerek kalanı bulduk. Bölmeyi yaparsanız kalanın 91 olduğunu görebilirsiniz. Şimdi sayılarımız 231 ve 91 oldu. 231’i 91’e bölersek kalan bu sefer 49 olacaktır. Şimdi 91 ve 49 için devam edelim.
91’in içinde 49 bir kere vardır ve kalan 42’dir. 49 ve 42 için devam edersek kalanı bu sefer 7 olarak buluruz. 7 x 6 tam olarak 42 olduğundan, bu bizim son adımımız. 1015 ve 231’in en büyük ortak böleni 7’dir.
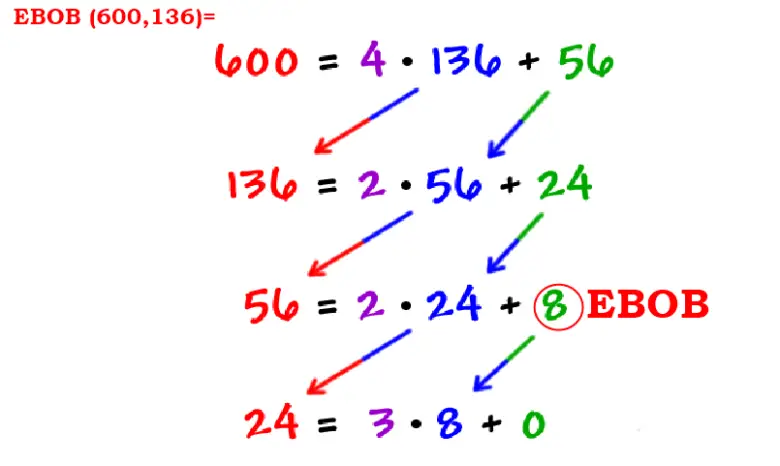
Bu Algoritma Nasıl Çalışıyor?
a > b olmak üzere iki a ve b sayısını ele alalım. O halde b > c olan bir n tam sayısı için a = n×b + c biçiminde yazabiliriz. Burada c sıfır ise sayının en büyük ortak böleni b sayısı olacaktır. Eğer c sıfır değilse, o zaman a ve b’nin herhangi bir ortak böleni c’yi de bölmelidir.
Dolayısıyla a ve b’nin en büyük ortak çarpanı c’yi de bölmelidir. Yani OBEB (a,b), b ve c’yi böler. Bu nedenle OBEB (b, c) ≥ OBEB (a, b) olmak zorundadır. Aynı zamanda OBEB (b, c) de a’yı bölmelidir. Yani, OBEB (a, b) ≥ OBEB (b, c) olur. Bu nedenle OBEB (a, b) = OBEB (b,c) olmalıdır.
Bu kalan bulma işlemini, sonunda sıfır kalanını elde edene kadar tekrarlayabiliriz. Bu durumda, orijinal a ve b sayı çiftinin en büyük ortak böleni (aslında süreçteki her sayı çifti için en büyük ortak bölen), süreçteki sıfır olmayan son kalandır.
Bu Algoritma Ne İşimize Yarar?
Elbette asal sayıları çarpanlarına ayırmak mümkün olduğunda ya da en büyük ortak bölenini bulmaya çalıştığınız sayılar küçük olduğunda geleneksel yöntemler ile ortak böleni hesaplamaya devam edin. Zaten okullarda veya sınavlarda karşınıza çıkacak sorular bu yöntem ile yapabileceğiniz biçimde ayarlanmış olacaktır. Ancak gerçek hayatta matematik, sınavlarda sorulan sorular için var olmaz.
Öklid algoritması aracılığı ile en büyük ortak böleni 1 bulduğumuz zaman sayıların ortak böleni olmadığını yani sayıların aralarında asal olduklarını söyleyebiliriz. Bu bilgi de asal sayılar ile uğraşmak zorunda kaldığımız pek çok alanda bilmek istenilen bilgilerden birisidir.
Ayrıca bu algoritma sadece en büyük ortak böleni bulmaya yaramaz. Aslında yöntemin ileri matematikte bir takım kullanımları vardır. Örneğin, a, b ve c’nin tamsayı olduğu ax + by = c doğrusal denklemlerinin tamsayı çözümlerini bulmak için kullanılan temel araçtır. Ek olarak bu algoritma, bilgisayar biliminin birçok alanında, özellikle kriptografi alanında bir temel taşıdır. Göz atmak isterseniz: Asal Sayılar Şifrelemede Neden ve Nasıl Kullanılır?
Kaynaklar ve ileri okumalar:
- Music and Euclid’s algorithm; yayınlanma tarihi: 1 Eylül 2006; Bağlantı: https://plus.maths.org/
- John Stillwell; Elements of Mathematics: From Euclid to Gödel ; Yayıncı: Princeton University Press
- Euclidean algorithm; Bağlantı: https://nrich.maths.org/1357
Size Bir Mesajımız Var!
Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak veya Patreon üzerinden ufak bir bağış yaparak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel