Bu yazıya konu olan soru, SAT (Scholastic Aptitude Test) sınavında bugüne kadar sorulmuş en zor matematik sorularından biri olarak kabul edilmektedir. Sorunun zorluk seviyesi o kadar yüksekti ki, sınava giren hiçbir öğrenci doğru cevabı bulamamıştı.

Daha da ilginci, soruyu hazırlayan uzmanlar bile çözüm konusunda tam bir fikir birliğine varamamıştı. Bu durum, yalnızca öğrenciler için değil, matematik alanında yetkin kişiler için de şaşırtıcıydı. Aşağıda, 1982 SAT sınavında sorulan soruyu orijinal haliyle paylaşıyoruz. Ardından, detaylı açıklamasını yaparak neden bu kadar zor olduğunu ele alacağız.
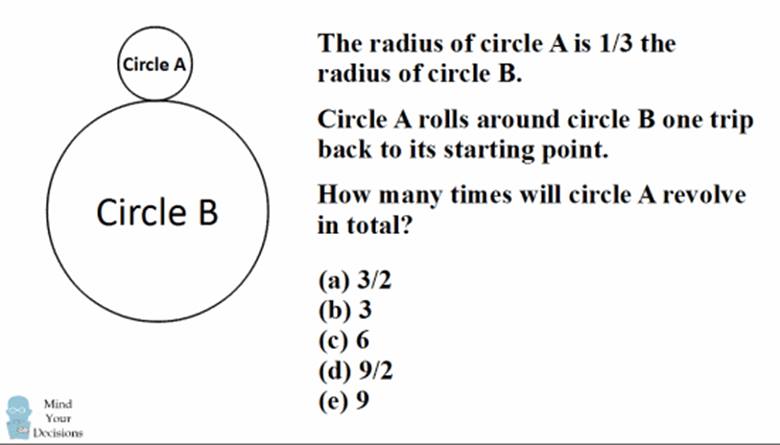
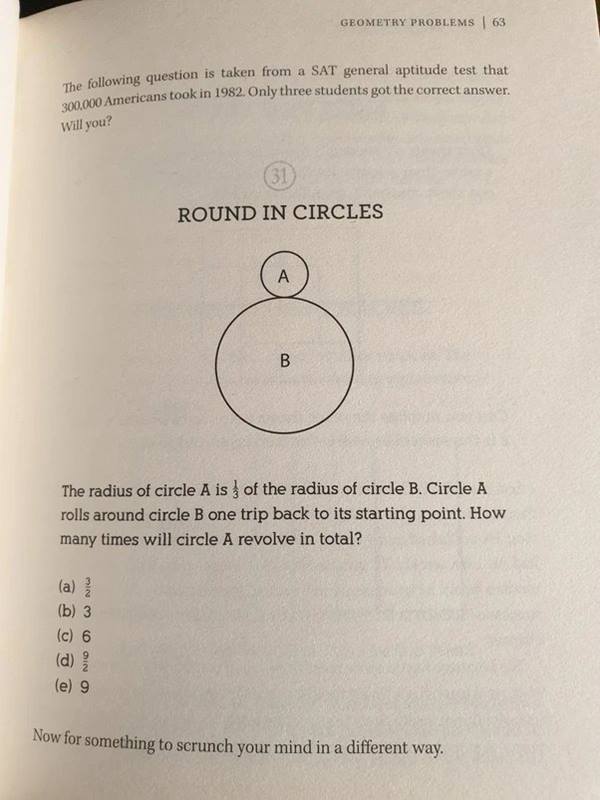
Şekilde, A çemberinin yarıçapı, B çemberinin yarıçapının üçte biri kadardır. A çemberi, başlangıç noktasından itibaren B çemberinin çevresinde kaymadan yuvarlanarak hareket etmeye başlar ve sonunda tekrar başlangıç noktasına ulaşır. Bunun için A çemberinin toplamda kaç tur atmalıdır?
Bu SAT Sorusu İle İlgili Sorun Nedir?
Bu sorunun cevabı, ilk bakışta size 3 gibi görünebilir. Sonuçta, B çemberinin yarıçapının, A çemberinin yarıçapının 3 katı olduğunu biliyoruz. Bu nedenle B çemberinin çevresi de A çemberinin çevresinin 3 katı olacaktır. Eğer küçük çemberi açıp büyük çemberin çevresine sarabilseydik, bunu tam 3 kez yapabilirdik.
Bu mantıkla hareket eden sınav sorusunu hazırlayanlar da doğru cevabın 3 olduğunu kabul etmişlerdi. Ancak bu yanlıştı. Üstelik işin ilginç yanı, diğer şıkların tamamı da yanlıştı. Sorunun asıl karmaşıklığı, A çemberinin yalnızca B çemberinin çevresinde yuvarlanmakla kalmayıp aynı zamanda kendi ekseni etrafında da dönmesiydi.
Bu sorunun doğru cevabı aslında 4’tü, ancak bu seçenekler arasında yer almıyordu. Sınava giren 300.000 öğrenciden yalnızca üçü, bu SAT sorusunda bir hata olduğunu fark etti ve durumu yetkililere bildirdi. Yapılan inceleme sonucunda, bu öğrencilerin haklı olduğu anlaşıldı ve tüm sınav kağıtları tekrar değerlendirildi.
Bu sorunun yarattığı şaşkınlık ve karmaşıklık nedeniyle, daha sonraki yıllarda “Coin Rotation Paradox” yani “Madeni Para Döndürme Paradoksu” olarak adlandırıldı. Bir problemin paradoks olarak nitelendirilmesi, sonucunun sezgilere aykırı olmasından kaynaklanır.
Madeni Para Döndürme Paradoksu nedir?

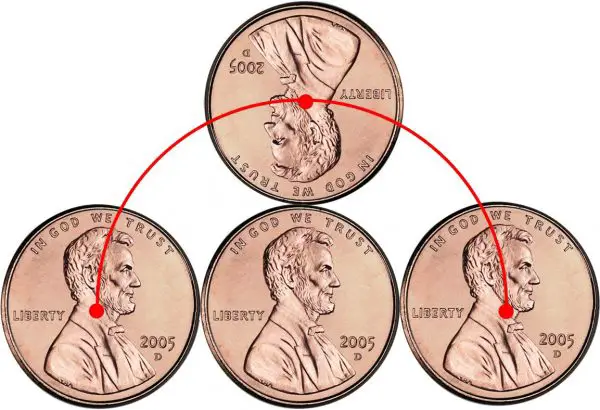
Bu soruyu biraz daha basitleştirelim. Bu kez, birbirinin tamamen aynı olan iki madeni para kullanacağız. Her iki parayı da masanın üzerine düz bir şekilde koyun. Şimdi, solda yer alan parayı, ok yönünde ortadaki paranın etrafında döndürdüğünüzü düşünün. Peki, işaretli yere ulaşana kadar tam tur mu, yoksa yarım tur mu dönecektir?
Çoğu kişi, paranın yalnızca yarım tur döneceğini düşünür. Ancak, aslında tam bir tur döner. Eğer bu cevaptan emin değilseniz, kendi madeni paralarınızla deneyebilirsiniz. Fakat denemeye üşeniyorsanız, sonucu şekil üzerindeki kırmızı çizgiyi takip ederek de görebilirsiniz.

Bu durumda, yukarıdaki şekle göre madeni para, başladığı noktaya geri dönene kadar toplamda iki tur atmış olacaktır. Bu sorunun cevabını anlamak için, öncelikle yuvarlanma hareketinin temel prensiplerini incelememiz gerekir.
İlk bakışta, paranın sadece bir tur atması gerektiği düşünülebilir, çünkü hareket ettiği mesafe, kendi çevresinin yalnızca bir katı kadar görünmektedir. Ancak, paranın yalnızca yüzey boyunca ilerlemekle kalmayıp aynı zamanda kendi ekseni etrafında da döndüğü göz önüne alındığında, ekstra bir dönüş meydana gelir.
Eğer madeni paramızın yarıçapını r kadar kabul edersek, paramızın merkezinin aldığı yol ( kırmızı çizgi) 1/2 x 2π x 2r=2πr kadar olacaktır. Bunun sonucunda paramızın merkezi etrafında bir tur tamamlaması için, para kendi etrafında iki defa dönmelidir. Aslında iki tane para ile bunu daha net görebilirsiniz.

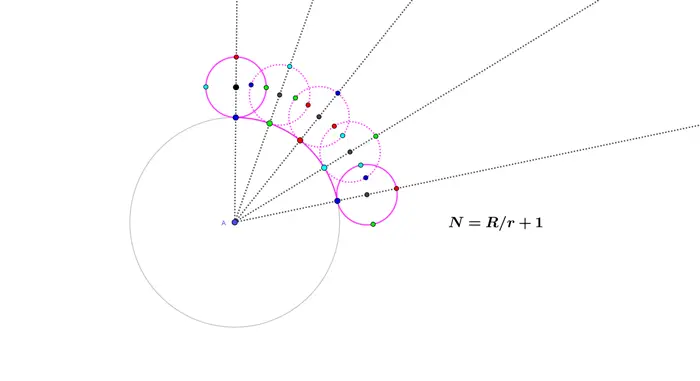
Bir çember, başka bir çemberin etrafında kaymadan yuvarlanıyorsa, hareketli çemberin kaç tur attığını bulmak için her zaman çemberlerin çevrelerini birbirine oranlamalı ve sonuca 1 eklemelisiniz.
Madeni Para Döndürme Paradoksunun Sonuçları SAT Sorusunun Ötesine Geçer
Güneş sistemini dışarıdan izleme şansını olsaydı, Dünya’nın bir yılda kendi etrafında dönüşünü kaç kez görürdünüz? Birçok kişi 365 ( tam olarak 365.24) dese de ama gerçek cevap 366 ( 366.24) olmalıdır.
Günlük yaşamımızda bir günü, Güneş’in gökyüzünde aynı konuma dönmesi için geçen süre olarak kabul ederiz. Yani, öğle saatlerinde Güneş’in her zaman doğrudan tepemizde olduğunu varsayarız. Ancak Dünya, kendi ekseni etrafında bir tam dönüşünü tamamladığında, Güneş gökyüzünde tam olarak önceki konumuna dönmemiş olur.
Bunun nedeni, Dünya’nın sadece kendi ekseni etrafında dönmekle kalmayıp aynı zamanda Güneş’in etrafında da hareket etmesidir. Dünya bir tam tur attığında, yörüngesinde de ilerlediği için Güneş’i tekrar aynı konumda görmek için ekstra bir dönüş daha yapması gerekir. Bu fark, Dünya’nın gerçek dönüş sayısının 366 olduğu anlamına gelir. Bu durumu daha iyi anlamak için aşağıdaki görseli incelemek faydalı olacaktır.
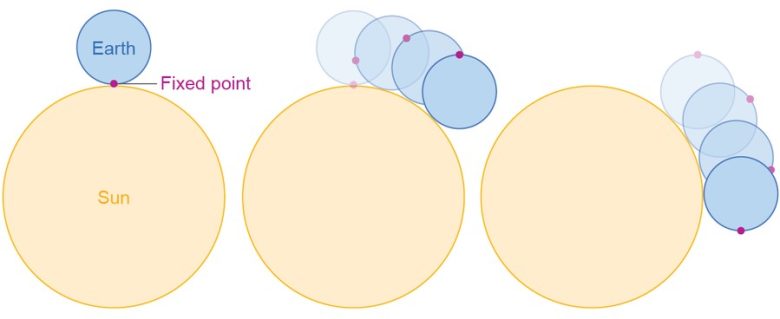
Şekilde, büyük daireyi Güneş, küçük daireyi Dünya ve üzerindeki kırmızı noktayı da gezegenimizde sabit bir yer olarak düşünelim. İlk durumda, soldaki kırmızı nokta için tam öğle vakti olduğunu kabul edelim.
Dünya kendi ekseni etrafında bir tam tur attığında, kırmızı nokta başlangıç konumuna geri döner. Ancak bu noktada yaşayan biri için hâlâ öğle vakti olmamıştır. Güneş, gökyüzünde önceki konumuna tam olarak dönmemiştir. Bunun gerçekleşmesi için Dünya’nın biraz daha hareket etmesi gerekir.
Dünya, kendi etrafındaki bir tam dönüşünü 23 saat 56 dakikada tamamlar.B u süre yıldız günü (sideral day) olarak adlandırılır. Ancak, Güneş’in gökyüzünde tepedeki konumuna geri dönmesi dört dakika daha sürer. İşte bu ek süre, günlük zaman hesaplamalarımızda kullandığımız ortalama 24 saatlik Güneş gününü oluşturur.
Eğer 1 Ocak 2024 tarihinde saat 12:00’de hem Güneş hem de yıldız gününü aynı anda ölçmeye başlasaydık, zamanla bu iki ölçümün birbirinden uzaklaştığını görürdük. 12 ay sonra, yani bir yılın sonunda, bu fark tam 24 saate ulaşır. 6 ay sonra, yıldız günü, Güneş gününün 12 saat önüne geçmiş olur.
Sonuç olarak
Hatalı bir SAT sorusu ve beraberinde birbirinin etrafında yuvarlanan bozuk paralar bize aslında zamanı dünyamızda ve uzayda nasıl hesapladığımızı da açıklamaktadır. Dünya’da yaşayan bizler için yıldız günü yerine Güneş gününü kullanmak daha mantıklıdır, çünkü günlük yaşamımızı Güneş’in hareketine göre düzenleriz.
Ancak astronomlar ve Dünya ile senkronize hareket etmek zorunda olan uydular için yıldız günü kritik bir öneme sahiptir. Gökyüzünde belirli bir noktaya her zaman aynı konumda bakmak isteyen bir gözlemci için, yıldız gününü baz almak gereklidir.
Kaynaklar ve ileri okumalar
- The SAT Problem That Everybody Got Wrong. Yayınlanma tarihi: 20 Haziran 2023. Kaynak iste: Scientific American. Bağlantı: The SAT Problem That Everybody Got Wrong
- The SAT Question Everyone Got Wrong. Yayınlanma tarihi: 30 Kasım 2023. Kaynak iste: Youtube/Veritasium. Bağlantı: The SAT Question Everyone Got Wrong
Size Bir Mesajımız Var!
Matematiksel, matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel