İlköğretim sıralarında devirli ondalık sayılarla tanışan öğrencileri şaşırtan sonuçlardan biri 0.99999…=1 ifadesidir. İlk bakışta kulağa pek mantıklı gelmez. Sonuçta bu iki değerin birbirine çok yakın olduğunu biliriz. Ancak çok yakın olmakla eşit olmak aynı şey değildir.

Bu noktada öğretmenler, tahtada bu eşitliğin neden doğru olduğunu açıklamaya başlar. Bazı matematiksel işlemler gösterirler ve her seferinde bu sonuçları haklı çıkarırlar. Böylece 0.99999… = 1 yazımının gerçekten doğru olduğuna kolayca ikna oluruz. Şimdi gelin, bu yöntemlere birlikte bakalım.
0.99999…=1 Gösterimi İle İlgili İspatlara Bakalım
0,99999… = 1 ifadesine dair en basit açıklamalardan biri, 1/3 = 0,33333… eşitliğiyle ilgilidir. Çünkü her iki tarafı da 3 ile çarptığınızda 3/3 = 0,99999… sonucuna ulaşırsınız. 3/3 ifadesi açıkça 1 olduğuna göre, buradan 0,99999…’un da bire eşit olduğu sonucu çıkar.
Bu açıklama ilk bakışta etkileyici görünse de, ne yazık ki bu bir ispat değildir. Hatta özünde bir mantık hatası barındırır. Çünkü 1/3 kesri tam olarak 0,33333… sayısına eşit değildir. Bu ifade, yalnızca işlem yapmayı kolaylaştırmak amacıyla kullandığımız yaklaşık bir değerdir.
Eğer x = 0.99999…, o zaman 10x = 9.99999… ve 9x = 9 ise x = 1
Öğretmenlerinizin bu konudaki bir diğer açıklaması — ki muhtemelen en sık duyduğunuz ve benim de zamanında derste kullandığım yöntem — aşağıdaki gibidir:
x = 0,99999…
10x = 9,99999…
10x – x = 9,99999… – 0,99999…
9x = 9
x = 1
Bu yöntemde dikkat çeken şey, sayının zorlu kısmının — yani sonsuza kadar tekrar eden kısmının — basit bir çıkarma işlemiyle ortadan kaldırılmasıdır. Böylece geriye sade ve anlaşılır bir ifade kalır ve işlem kolaylıkla tamamlanır.
Ancak burada biraz durup düşünmek gerekir. Çünkü çıkarma işlemini yaptığımız iki sayı da sonsuz basamaklıdır. Sonsuzlukla işlem yaparken dikkatli olunmalıdır. Küçük bir ihmal bile bizi hataya götürür. Bu yöntem sezgisel olarak ikna edicidir ve öğretim açısından işe yarar. Fakat teknik anlamda bir ispat değildir. Bu yüzden, konuyu anlatırken bu farkı vurgulamak önemlidir.
İşin İçine Limit Ve Sonsuz Serileri Sokarsak
Matematikte geometrik seri, ardışık terimler arasında sabit bir oran bulunan seridir. Yinelenen bir ondalık sayı, ortak oranı 1/10’un bir kuvveti olan bir geometrik seri şeklinde düşünülebilir. Bir geometrik serinin ilk n teriminin toplamı ise aşağıdaki biçimde hesaplanır.

Buraya kadar anlattıklarımız size tanıdık gelmiş olabilir. Belki de “Bunları zaten biliyordum” diye düşündünüz. Gerçekten de, aktarılan üç yaklaşım da kendi içinde tutarlıdır. İlk iki yöntem sezgisel açıklamalara dayanır. Sonuncusu ise, devirli ondalık sayıların matematiksel tanımını temel alır ve daha sağlam bir zemine oturur.
Çoğu kişi için bu açıklamalar yeterli olacaktır. Ama eğer siz de “Bu iki ifadenin tam olarak eşit olduğunu daha kesin biçimde göstermek mümkün mü?” diye soruyorsanız, okumaya devam etmenizde fayda var. Birbirinden farklı olan iki şeyin neden aynı kabul edildiğini anlamak için de gerçek üstü reel sayılar ile tanışmanız gerekecektir.
Gerçek Cevap: Hipergerçek Sayılar
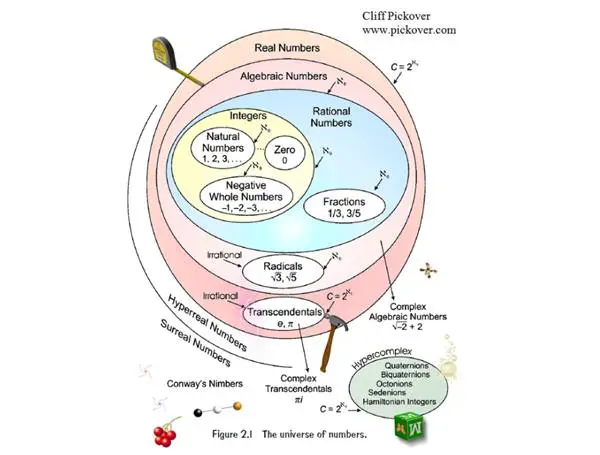
Hipergerçek sayılar (hyperreal numbers), gerçek sayıların bir uzantısıdır. Yani, yalnızca gerçek sayılar kullanarak 0,99999… ≠ 1 olduğunu ispatlamanın mümkün olmadığını söyleyen kısıtlama, hipergerçek sayılar için de geçerlidir. Ancak hipergerçek sayıların burada önemli bir işlevi vardır: Bu sayı sistemi, bizim kusurlu ondalık gösterim sistemimiz içinde sonsuz küçük (infinitesimal) değerleri temsil etmenin bir yolunu sunar.

Kalkülüsün icadının ardından, sonsuz küçük niceliklere dayanan bu yöntemin matematiksel tutarlılığıyla ilgili ciddi endişeler devam etti. 1800’lü yıllarda Bolzano, Cauchy ve Weierstrass, limit ve süreklilik kavramlarını ε–δ (epsilon-delta) tanımıyla yeniden yapılandırarak bu soruna kalıcı bir çözüm getirdiler.
ε–δ (epsilon-delta) biçimindeki formalizmde, limitler şu şekilde tanımlanır: Bir dizi {xn} için, bu dizinin limiti x’tir. Her pozitif ε için, ne kadar küçük olursa olsun, öyle bir N sayısı bulunabilir ki, n>N olduğunda ∣xn−x∣<ε olur. Bu tanımdan sonra türev, alışık olduğumuz şu biçimde tanımlanacaktır.
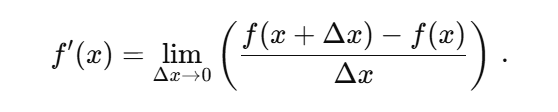
Bu gösterim biçimi, matematik öğrencilerinin nesiller boyunca zorluk yaşadığı bir konu olmuştur. Peki bundan kaçınmanın bir yolu var mı?
1960’larda Abraham Robinson, bildiğimiz gerçek sayılar sisteminin hipergerçek sayılar adı verilen çok daha geniş bir kümeye genişletilebileceğini gösterdi. Hipergerçek sayılar sistemi R* ile gösterilir. Bu sayı sistemi tüm gerçek sayıları içerdiği gibi, ayrıca sonsuz küçük ve sonsuz büyük sayıları da içerir.
Hipergerçek sayıları tanımlamak için kullanılan aksiyomlardan biri, en az bir adet sonsuz küçük sayı ε’nin var olduğudur. Sonsuz küçük bir sayının çarpma işlemine göre tersi sonsuz büyük bir sayı olur. Bu sayı 1/ε ifadesiyle gösterilir.
0.99999…=1 Gösterimi Hipergerçek Sayılar ile Tutarlıdır
Hipergerçek sayıların önemli işlevi, kusurlu ondalık gösterim sistemimiz içinde sonsuz küçük değerlerin temsil edilebilmesini sağlamalarıdır. Bu sayede, aslında hepimizin sezgisel olarak doğru bildiği bir şeyi matematiksel olarak ifade etmek mümkün hâle gelir. Hepimiz biliriz ki 0,99999… tam olarak 1’e eşit değildir. Ancak aralarındaki fark o kadar sonsuz küçüktür ki “önemli sayılmaz.”
Bu düşünceyi doğru biçimde ifade eden matematiksel gösterim şudur: 1 − h = 0,99999… Buradaki h, hipergerçek sayı sisteminde tanımlanan sonsuz küçük bir değerdir. Ve bu ifade, 1 ile 0,99999… arasında gerçek bir eşitlik olmadığını ortaya koyar.
Aynı durum 1/3 ile 0,33333… arasındaki ilişki için de geçerlidir. 1/3 ifadesi hipergerçek sayılarla şu şekilde yazılır: 1/3 − h = 0,33333… Bu da, 1/3’ün 0,33333…’e yalnızca sonsuz küçük bir farkla yaklaştığını ama tam anlamıyla eşit olmadığını açıkça gösterir.
Sonuç Olarak
0,99999… hiçbir zaman tam olarak 1’e eşit olmadı. Bunun yerine, ondalık sayıların gösterimindeki bir sınırlama, bu iki sayının eşit olduğu yanılsamasını yarattı. Her şeyi düzenli ve tutarlı kılma arzusu ise, akademik bir doğrulama yanlılığına yol açtı.
Bu durumdan çıkarılacak ders? Her şeyi ve herkesi sorgulayın — uzmanları bile. Eğer bir şey size yanlış geliyorsa ve sunulan “ispatlar” sizi ikna etmiyorsa, araştırmaya devam edin. Çünkü belki de gerçekten doğru bir şeyin peşindesinizdir.
Kaynaklar ve ileri okumalar
- Proof that .99999… is NOT equal to 1. yayınlanma tarihi: 12 Mayıs 2018; Bağlantı: https://medium.com/
- I’m Settling This Math Debate Forever (.99 repeating = 1). Yayınlanma tarihi: 17 Mayıs 2021; Bağlantı: https://www.youtube.com/
- A Friendly Chat About Whether 0.999… = 1 Bağlantı: https://betterexplained.com/
Size Bir Mesajımız Var!
Matematiksel, matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel





